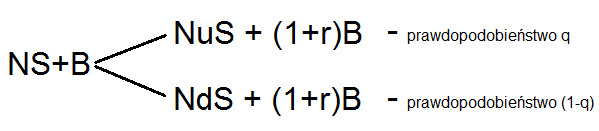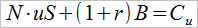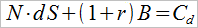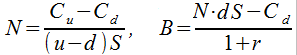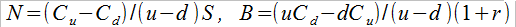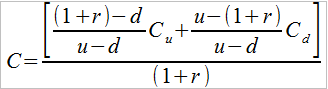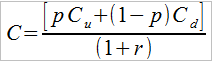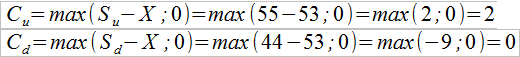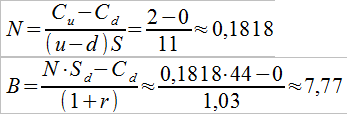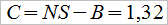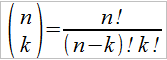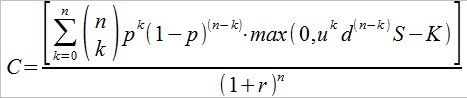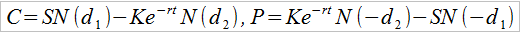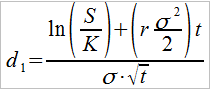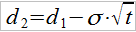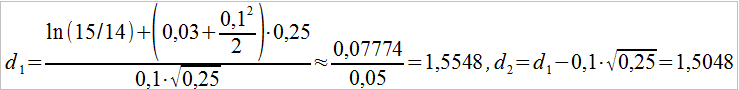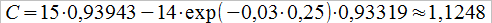Wycena opcji - dwa modele

Przyjrzymy się dziś podstawowym metodom i wzorom dotyczącym wyceny opcji finansowych. W kolejnych tekstach pokażemy zastosowanie opisanych sposobów przy wycenie opcji rzeczowych.

Tak naprawdę dwa podstawowe podejścia, które są stosowane, to model dwumianowy i model Blacka-Scholesa. W obu przyjmuje się dość mocne założenia na temat rynku – założenia, które oczywiście pozwalają uprościć obliczenia, ale też do pewnego stopnia oddalają wyniki od rzeczywistości.

Uniwersalne aksjomaty, przyjmowane przy obu metodach, są takie: 1) oprocentowanie kredytów i depozytów jest jednakowe; 2) kredyty można zaciągać w nieograniczonym zakresie; 3) obrót instrumentami jest dostatecznie płynny; 4) nie uwzględnia się kosztów transakcji oraz podatków; 5) walory można bez przeszkód i dowolnie dzielić na mniejsze części; 6) można stosować krótką sprzedaż.

Zacznijmy od modelu dwumianowego dla opcji kupna (call). To, jak zmienia się w nim cena akcji, prezentuje się zwykle w postaci drzewa. Zakłada się, że ceny zmieniają się w pewnej skończonej liczbie okresów, a do tego okresy te są równe. Co więcej, w każdym okresie cena waloru, na który wystawiono opcję (zwykle – akcji) rośnie o taki sam procent – lub spada o taki sam procent.

W modelu dwumianowym rozpatrzmy najpierw wersję jednookresową. A zatem będziemy mieli tylko jedną "turę", jeden "ruch" – cena akcji wzrośnie lub spadnie. Cenę bieżącą, wyjściową naszej akcji określamy jako S. Może ona w jednej turze wzrosnąć według stopy u (wynoszącej np. 1,5 – wtedy po zmianie będziemy mieli cenę uS = 1,5*S) – lub spaść według stopy d (np. d = 0,7 – w takim układzie będziemy mieli dS = 0,7*S).

Wygląda to tak:

Jak widać, każdy ruch może odbyć się z określonym prawdopodobieństwem. Naturalnie prawdopodobieństwa te sumują się do 1. To, co pokazuje nam ów schemat, to jednak dopiero zmiana ceny instrumentu. A co dzieje się z opcją call? Niech C oznacza jej bieżącą cenę (w gruncie rzeczy jest to właśnie niewiadoma, którą chcemy wyznaczyć). Niech C_u oznacza max (0, uS – K), zaś C_d będzie równe max (0, dS – K). Są to więc wartości opcji po jednym okresie, gdy K to cena wykonania opcji. Uzasadnieniem dla tych definicji są znane właściwości opcji call względem jej ceny wykonania.

Co teraz? Otóż cała koncepcja opiera się na tym, że chcemy opracować replikację opcji przy pomocy innego portfela, złożonego z pewnej liczby (ozn. N) akcji (właśnie tych, które są instrumentem bazowym opcji) oraz B – czyli kredytu bankowego lub obligacji. Wartość B może być dodatnia lub ujemna, czasami rozpatruje się po prostu wariant ujemny, pojmując B jako pożyczkę zaciągniętą w celu zakupu akcji. Ogólnie jednak koszt inwestycji replikującej wynosi: NS + B. Zakłada się tu stopę wolną od ryzyka wynoszącą r (przy czym musi być u > 1+r > d) i stąd po rozpatrywanym okresie (po wykonaniu "tury") sytuacja będzie taka:

Żądamy następujących zależności:

W ten sposób wartość portfela replikującego będzie zrównoważona z ceną opcji kupna. Z układu powyższego wyliczamy N oraz B:

Uwaga! Możemy te wzory przedstawić też tak:

W obu ujęciach prawe strony składają się tylko z wartości już znanych. A gdzie to, czego naprawdę szukamy, czyli C? Otóż musimy założyć, że NS + B = C, a stąd mamy C = NS – B. W drugiej wersji – dokonując odpowiednich przekształceń – otrzymujemy tzw. wzór Sharpe'a:

Oznaczając współczynnik stojący przy C_u literką p (wielkość tę nazywa się prawdopodobieństwem neutralizującym ryzyko) otrzymujemy często spotykany zapis:

Dokonajmy przykładowego przeliczenia:

Załóżmy, że mamy aktywo bazowe (np. akcję), której cena to obecnie 50 zł. W następnej turze może ona wzrosnąć do poziomu Su równego 55 zł (a więc czynnik u to 1,1) lub spaść do 44 zł (d = 0,88). Niech ceną wykonania opcji kupna będzie kwota X = 53 zł, przyjmijmy też stopę wolną od ryzyka na poziomie r = 3 proc.

Takie będą wartości opcji w dniu jej wygaśnięcia, tj. po jednym okresie:

Chcemy znaleźć portfel replikujący. Zastosujemy tutaj wyprowadzone już wzory:

Stąd natomiast otrzymujemy wartość:

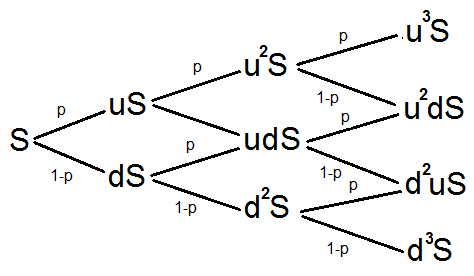
Naturalnie to na razie bardzo prosty model. Wypada powiedzieć coś o sytuacji wielookresowej, czyli wyglądającej np. tak (tu akurat n = 3):

Naturalnie łatwo wyobrazić sobie, jak będzie wyglądał odpowiednik tego diagramu dla opcji, a nie instrumentu bazowego; np. w miejsce S będzie C, w miejsce u²S wpiszemy C_uu – itd. Można zastosować tutaj indukcję wsteczną. A zatem znając wartości na samych końcach, możemy obliczyć wcześniejsze węzły. Na przykład, gdyby n było równe 2, to wówczas C_u obliczymy tak, jak wcześniej obliczaliśmy C, tyle że teraz skorzystamy z C_uu oraz C_ud. Analogicznie policzymy C_d. Rzecz jasna takie rozumowanie wypada uogólnić. Zauważmy, że sposobów dojścia do każdej ceny (np. do d²S) jest tyle:

Przy czym n to liczba kroków (okresów), zaś k – to liczba ruchów "w górę". Pozostawiając wszystkie inne oznaczenia takie, jakie były wcześniej, otrzymujemy następujący wzór na cenę europejskiej opcji kupna w modelu dwumianowym:

Przy opcji sprzedaży wzór będzie właściwie taki sam, tyle że będziemy mieli max(0, K – u^kd^(n-k)S).

Inne podejście – inne niż dwumianowe – to tzw. model Blacka-Scholesa, przedstawiony w roku 1973 przez Fischera Blacka i Myrona Scholesa. Radzi on sobie z pewnymi ograniczeniami ujęcia dwumianowego, choć z drugiej strony przyjmuje inne, mocne założenia – na przykład to, że stopy zwrotu z aktywa bazowego w nieskończenie małych jednostkach czasu mają rozkład normalny o stałej średniej i odchyleniu standardowym.

Wzór wyprowadza się w oparciu o teorię procesów stochastycznych, teorię równań różniczkowych i tzw. lemat Ito (wątki te pominiemy tutaj – rozpisanie całego rozumowania nie jest bynajmniej banalne).

Ostateczne rozwiązanie wygląda tak:

Przy czym oznaczenia są takie:

C, P – odpowiednio ceny opcji kupna i sprzedaży (europejskiej)

S – bieżąca wartość akcji (ogólnie: aktywa bazowego)

N(d) – wartość dystrybuanty dla ustandaryzowanego rozkładu normalnego przy argumencie d – a zatem prawdopodobieństwo, że zmienna losowa o takim rozkładzie przybierze wartość nie większą niż d.

K – cena wykonania opcji

t – czas, jaki pozostał do wygaśnięcia opcji - jako ułamek roku (np. półrocze to 0,5)

Ale to nie wszystko, mamy bowiem też:

Gdzie:

σ – odchylenie standardowe ceny instrumentu bazowego.

Widać zatem, że całe przedsięwzięcie, jeśli rzecz liczyć na kartce – nawet z pomocą kalkulatora i tablic rozkładu normalnego – jest dość złożone. Tym niemniej sporo we współczesnych czasach robią w tej kwestii komputery, a ogólnie rzecz biorąc, model Blacka-Scholesa jest powszechnie znany, nauczany i stosowany.

I jeszcze przykład zastosowania: załóżmy, że mamy akcję, która obecnie kosztuje 15 zł (S = 15). Niech cena wykonania będzie równa K = 14 zł. Przyjmijmy też r = 3%, σ = 0,1, zaś czas do wygaśnięcia opcji niech wynosi 3 miesiące, tj. t = 0,25 (jedna czwarta roku).

Liczymy:

Z tablic mamy: N(d1) = 0,93943, N(d2) = 0,93319.

A zatem:

Oto i otrzymany wynik.

B. Garga

Bibliografia:

R. Ziarkowski, Opcje rzeczowe oraz ich zastosowanie w formułowaniu projektów inwestycyjnych, Wydawnictwo Akademii Ekonomicznej w Katowicach 2004.

W. Rudny, Opcje rzeczowe w procesie tworzenia wartości przedsiębiorstwa, Wydawnictwo Akademii Ekonomicznej w Katowicach 2004.

M. Skwara, Opcje rzeczowe: nowe spojrzenie na wycenę, w: Wycena i zarządzanie wartością firmy, praca zbiorowa pod red. A. Szablewskiego i R. Tuzimka.

W. Dębski, Rynek finansowy i jego mechanizmy, PWN 2014.