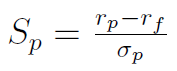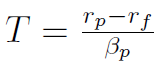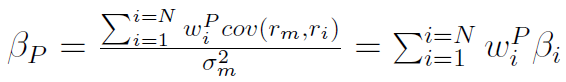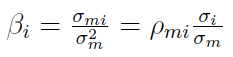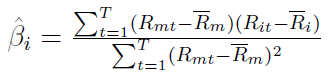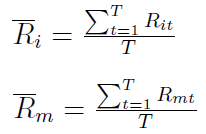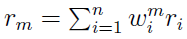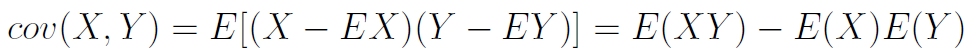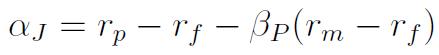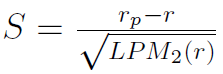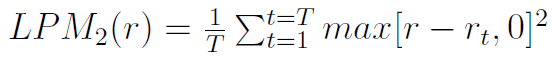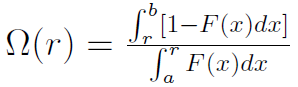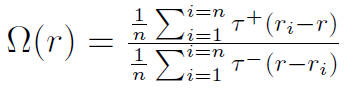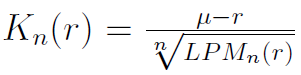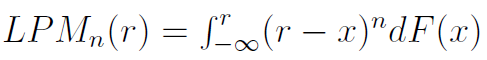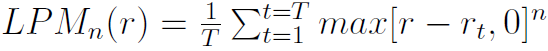Miary efektywności portfela

W poniższym opracowaniu przedstawimy kilka narzędzi, przy pomocy których analitycy finansowi oceniają efektywność inwestycji w portfele aktywów - np. akcji.

Bodaj najpopularniejszą, a także dość prostą metodą jest tzw. wskaźnik Sharpe'a. Pokazuje on wysokość premii, która przypada inwestorowi w stosunku do ponoszonego przezeń ryzyka. Nie będziemy tu szczegółowo wyprowadzać i uzasadniać wzoru. Bazuje on w każdym razie na modelu wyceny CAPM, a ostatecznie wygląda następująco:

Przez r_p rozumiemy średni zwrot z portfela w badanym okresie, tzn. średnią ważoną stóp zwrotu poszczególnych składników, gdzie wagą jest udział danego składnika w całkowitej kapitalizacji. Portfel może zawierać zarówno aktywa ryzykowne (np. akcje), jak i pozbawione ryzyka (jak obligacje). Z kolei r_f to średnia stopa zwrotu z inwestycji w pełni wolnej od ryzyka, czyli np. z bonów skarbowych. Mianownik wzoru to odchylenie standardowe stopy zwrotu portfela w analizowanym czasie.

Wskaźnik mówi nam, o ile stopa zwrotu przewyższa stopę porównawczą (wolną od ryzyka), biorąc jednak pod uwagę zmienność notowań naszego funduszu aktywów (stąd dzielenie przez odchylenie standardowe). Im wyższy rezultat, tym lepiej.

Narzędzie to można zmodyfikować, budując tzw. wskaźnik Treynora (przedstawiony w roku 1965 przez J. Treynora w pracy How to rate management of investment funds). Wygląda on tak:

Licznik ułamka się nie zmienił, ale u dołu mamy β_p, czyli współczynnik beta dla portfela. Jak wyliczana jest ta wielkość? Opisuje to następujący wzór:

Współczynnik beta dla portfela jest zatem sumą współczynników beta poszczególnych akcji (β_i) przemnożonych przez wagi w_i^P, tzn. udziały tychże kolejnych aktywów w portfelu. Na przykład 1/3 portfela mogą stanowić akcje jednej firmy, a 2/3 - akcje drugiej.

Współczynnik beta - tak dla jednej akcji, jak i dla portfela - ma pewną standardową interpretację. Jeśli jest większy od 1, to znaczy, że stopa zwrotu akcji rośnie (spada) bardziej (w sensie: o więcej w przyjętych jednostkach, zwykle punktach procentowych) niż rośnie (spada) stopa zwrotu wskaźnika rynku. Tą ostatnią może być np. indeks rynku (taki jak indeksy giełdowe w rodzaju WIG czy WIG20).

Gdy β należy do (0, 1), to wtedy stopa zwrotu akcji rośnie (spada) o mniej niż rośnie (spada) stopa zwrotu indeksu rynku. Wówczas akcję nazywa się defensywną, podczas gdy we wcześniejszym przypadku mówimy o akcji agresywnej.

Gdy β = 1, to znaczy, że akcja w przeciętny sposób reaguje na zmiany rynkowe, a jeśli β = 0, to w ogóle nie reaguje. Taka sytuacja zachodzi - przynajmniej teoretycznie - w przypadku instrumentu wolnego od ryzyka, jak bon skarbowy. Jeśli β < 0, to zależności pomiędzy wzrostem (spadkiem) wartości akcji a wzrostem (spadkiem) indeksu giełdowego jest odwrotna - stopa zwrotu z waloru rośnie, gdy spada indeks i vice-versa. Przypadki takie są rzadkie.

Skąd jednak wziąć poszczególne bety? Ogólny wzór w modelu rynkowym Sharpe'a jest następujący:

Przez σ_mi rozumiemy kowariancję pomiędzy stopą zwrotu z portfela rynkowego a stopą zwrotu z i-tej akcji. Z kolei ρ_mi to współczynnik korelacji między stopą zwrotu z portfela rynkowego a stopą z i-tej akcji.

Problem w tym, że te parametry tak naprawdę nie są nam znane. W rzeczywistości trzeba więc β_i estymować. Można wykazać, że nieobciążony estymator wygląda tak:

Zakładamy przy tym, że:

Jak można się domyślić, R_it (R_mt) to - odpowiednio - stopy zwrotu z i-tej akcji lub z całego rynku w okresie t, np. w dniu t. T to liczba okresów (dni, tygodni), które bierzemy pod uwagę w naszych dociekaniach.

*

Jeżeli r_i to stopa zwrotu z i-tej akcji, wtenczas przez r_m rozumiemy średnią ważoną stóp zwrotu z poszczególnych aktywów (akcji, bo możemy ograniczyć się do nich dla ustalenia uwagi). De facto może to być po prostu stopa zwrotu z indeksu, jak to wspomnieliśmy wyżej. Przez w_i^m rozumiemy udział i-tej akcji w kapitalizacji portfela rynkowego (czyli np. to, jaki jest udział spółki w WIG20 czy DAX, jeśli taki indeks bierzemy pod uwagę). Stąd można zapisać:

Z kolei cov, czyli kowariancja dwóch zmiennych losowych, wyraża się w ogólności takim wzorem (gdzie E(X) to wartość oczekiwana zmiennej X):

Wskaźnik Treynora jest, podobnie jak wskaźnik Sharpe'a, tym większy, im większa jest premia za ryzyko.

Można też wyliczyć tzw. alfę Jensena:

Portfel, dla którego alfa ta jest równa 0, nazywamy dobrze wycenionym. Jego cena rynkowa jest równa cenie oszacowanej przez model CAPM. Niedowartościowany jest portfel, dla którego alfa jest mniejsza od zera, zaś przewartościowany - ten, dla którego wartość jest wyższa od zera.

*

Następny wynalazek to miara Sortino:

W liczniku mamy nadal r_p (średni zwrot z portfela w danym okresie), ale za r przyjmujemy tzw. MAR - minimalną stopę zwrotu akceptowaną przez inwestora. Wielkość LPM_2 to tzw. dolny moment cząstkowy drugiego rzędu, na podstawie danych empirycznych (przy T obserwacjach stopy zwrotu) liczony tak:

W powyższym wzorze r_t to właśnie stopa zaobserwowana (osiągnięta) w okresie t-tym. Wskaźnik ten tym różni się od wzoru Sharpe'a, że zamiast odchylenia standardowego bierze pod uwagę tzw. semiodchylenie, które bierze po uwagę tylko odchylenia ujemne, tj. in minus, od minimalnej wymaganej stopy zwrotu). Wynika to z tego, że wskaźnik Sharpe'a opiera się na założeniu, że rozkład stóp zwrotu jest normalny i stąd też symetryczny. Tymczasem na wielu rynkach (np. na GPW według badań K. Piontka z lat 2003 - 2006) można znaleźć wiele akcji, dla których rozkład stóp zwrotu cechuje się mniejszą lub większą skośnością.

*

Kolejne narzędzie to miara Omega:

Wskaźnik ten przedstawiony został w pracy C. Keatinga i W. F. Shadwicka zatytułowanej A Universal Performance Measure, opublikowanej nie tak dawno, bo w roku 2002. W pierwszej wersji pracy autorzy nazywali swój wynalazek wskaźnikiem Gamma.

Przez F(x) rozumiemy dystrybuantę stóp zwrotu z portfela. Z kolei r (czasami używa się oznaczenia L) to wartość progowa stopy zwrotu - w szczególności może być to stopa wolna od ryzyka. Całkowanie może teoretycznie odbywać się od -∞ do r oraz od r do +∞. Wystarczy nam jednak (a, b) jako przedział dopuszczalnych stóp zwrotu.

Funkcja ta jest ciągła i malejąca na (a, b), poza tym przyjmuje dodatnie wartości rzeczywiste. W punkcie równym średniej stopie zwrotu za badany okres przyjmuje wartość 1.

Na podstawie danych empirycznych Omegę estymuje się tak:

Gdy r_i - r > 0, to τ⁺ = 1, τ^- = 0 - a gdy r_i - r mniejsze lub równe od zera, to przyjmujemy odwrotne oznaczenia. Symbolem r_i nadal oznaczamy stopę zwrotu z i-tej akcji w portfelu. A zatem Omega to iloraz wartości oczekiwanej zysków przez wartość oczekiwaną strat - względem porównawczej wielkości (stopy) r.

Zasadnicza interpretacja nie jest zawiła: im wyższa wartość Omegi, tym lepiej. Oczywiście do tego dochodzi wiele rozważań - np. na temat tego, jak Omega reaguje na zmiany różnych charakterystyk rozkładu, takich jak kurtoza czy skośność - ale nie będziemy tu o tym mówić.

*

Mamy też następujące narzędzie: tzw. miarę Kappa, wprowadzoną przez P. D. Kaplana i J. A. Knowlesa w pracy Kappa: A Generalized Downside Risk-Adjusted Performance Measure. Wzór prezentuje się następująco:

Przez μ rozumiemy oczekiwaną w danym okresie stopę zwrotu, r to minimalna żądana stopa zwrotu. U dołu mamy znaną już wielkość LPM - tylko że tym razem w postaci ogólniejszej, bo jest to n-ty dolny moment cząstkowy (wprowadzony w roku 1991 przez Harlowa). Może być on liczony w sposób ciągły, przez całkę - lub dyskretnie, na podstawie danych empirycznych:

Miara Sortino jest, jak łatwo zauważyć, szczególnym przypadkiem Kappy - dla n = 2. Kappa dla każdego n jest monotonicznie malejącą funkcją zmiennej r, czyli progowej wartości stopy zwrotu. Kappa dla n = 1, powiększona o liczbę 1 - to nic innego jak analizowana wyżej Omega. Im wyższe wartości Kappy przy określonym n, tym lepsza inwestycja.

Adam Witczak

BIBLIOGRAFIA:

K. Pera, R. Buła, D. Mitrenga, Modele inwestycyjne, C. H. Beck, Warszawa 2014.

M. Jadamus-Hacura, Miary oceny efektywności zarządzania portfelami, w: Metody matematyczne, ekonometryczne i komputerowe w finansach i ubezpieczeniach 2007, praca zbiorowa pod red. P. Chrzana i T. Czernika, Wydawnictwo Akademii Ekonomicznej w Katowicach 2009

A. Kopiński, Analiza polskich funduszy inwestycyjnych w okresie 2009 - 2012 (miernik rozwoju Hellwiga na tle innych metod), Annales Universitatis Mariae Curie-Sklodowska, vol. XLVII, 3, 2013

M. Pichura, Miernik Omega jako wszechstronna miara efektywności inwestycji, Uniwersytet Ekonomiczny w Katowicach

C. Keating, W. F. Shadwick, A universal performance measure, The Journal of Performance Measurement, 2002, Spring.

P. D. Kaplan, J. A. Knowles, Kappa: A Generalized Downside Risk-Adjusted Performance Measure, Journal of Performance Measurement, 2004, No 8 (3).

K. Jajuga, K. Kuziak, P. Markowski, Inwestycje finansowe, Wydawnictwo Akademii Ekonomicznej im. Oskara Langego we Wrocławiu, Wrocław 1998.

W. Tarczyński, "Rynki kapitałowe. Metody ilościowe, vol. II", AW Placet 1997.