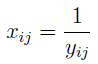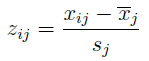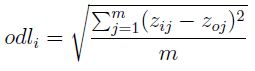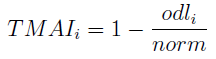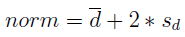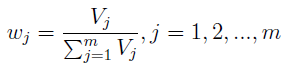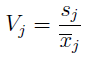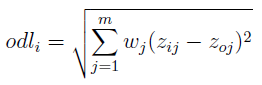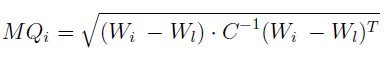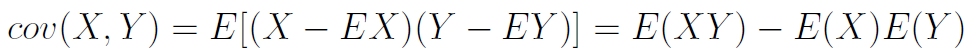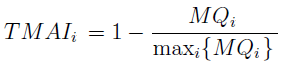Miara TMAI przy badaniu spółek

Zaczniemy od uwagi niewątpliwie prawdziwej, ale nieco banalnej: otóż istnieje naprawdę wiele rozmaitych sposobów porównywania spółek między sobą. Analiza wskaźnikowa, portfelowa czy techniczna to działy, które obfitują w tego rodzaju narzędzia. W jednych stosuje się proste ułamki i nierówności, w innych bada się wykresy kursu akcji, a w jeszcze innych uruchamia się zaawansowane metody z obszaru probabilistyki, statystyki czy programowania matematycznego.

Miara TMAI jest stosunkowo prostym narzędziem, zwłaszcza jeśli pojmiemy intuicję, jaka za nią stoi. TMAI to skrót od pojęcia 'taksonomiczna miara atrakcyjności inwestycji'.

Rzecz sprowadza się do analizy wskaźnikowej i dość podstawowej statystyki (choć zagadnienie można komplikować, jak to zwykle bywa w matematyce). Otóż wyobraźmy sobie, że dla danego przedsiębiorstwa obliczyliśmy szereg wskaźników - np. indeksy płynności bieżącej, zwrotu z kapitału własnego, rentowności netto etc. Niewątpliwie można wówczas przedstawić uzyskane wyniki w formie wektora (wierszowego czy kolumnowego, wygodniej chyba myśleć o tym drugim ujęciu).

W algebrze wektorów można jednak określić normę - a następnie metrykę, tj. odległość pomiędzy nimi. Moglibyśmy zatem przyjąć, że dwie firmy są w pewien sposób podobne, jeśli odpowiadające im wektory wskaźników są blisko siebie. W metodzie TMAI bada się jednak nieco inne zagadnienie - mianowicie ustala się pewne modelowe, wzorcowe przedsiębiorstwo, które ma najlepsze wartości wskaźników, a następnie bada się odległość pomiędzy nim a pozostałymi spółkami. Im dalej jakaś firma - tym gorzej, tym bardziej odbiega od wzorca.

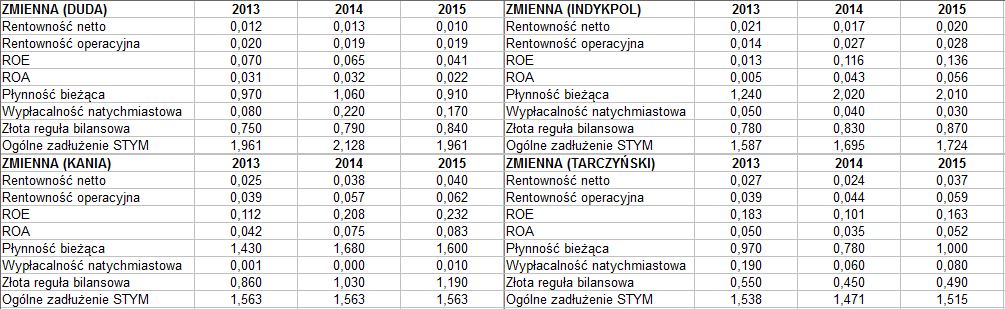
W dalszym ciągu będziemy równolegle prezentować teorię i pewien prosty przykład praktyczny. Weźmiemy pod uwagę cztery przedsiębiorstwa mięsne z głównego rynku akcyjnego warszawskiej GPW. Nasi protagoniści to Duda (obecnie Gobarto, ale rozpatrujemy dane archiwalne), Indykpol, Henryk Kania i Tarczyński. Interesować będą nas wskaźniki opracowane na podstawie raportów rocznych (skonsolidowanych tam, gdzie takie publikowano) z lat 2013 - 2015.

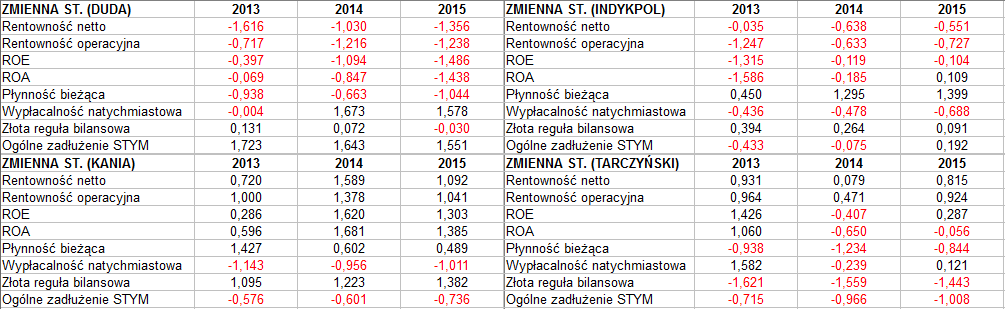
Spójrzmy:

Zastosowaliśmy 8 wskaźników (czy też zmiennych lub cech). Niektóre z nich zwyczajowo przedstawia się w postaci procentowej, ale tu wszystko sprowadziliśmy do ułamków dziesiętnych. Np. rentowność netto 0,041 oznacza 4,1 proc. ROA na poziomie 0,032 to zwrot równy 3,2 proc.

Pierwsza uwaga: w wierszu 'ogólne zadłużenie' mamy dopisek STYM i wartości daleko wyższe od 1. O co chodzi? Otóż w naszym modelu mamy zasadniczo dwa typy zmiennych. Jedne to stymulanty - im wartość jest wyższa, tym lepiej. Drugie to destymulanty. Zadłużenie jest destymulantą - cieszymy się, jeśli jest niskie. Ale w takim razie cieszymy się też, jeżeli jego odwrotność jest wysoka. To, co widzimy w tabeli, to właśnie odwrotność zadłużenia. Inaczej mówiąc, destymulantę y_ij (i-ta spółka, j-ta zmienna) przekształcamy w stymulantę przy pomocy takiego wzoru:

Dodajmy jeszcze, że uprościliśmy zagadnienie. Mianowicie tak naprawdę nie zawsze jest tak, że im wyższa stymulanta, tym lepiej. Pisaliśmy swego czasu o tym, że np. płynność bieżąca czy wypłacalność natychmiastowa mogą być niekiedy zbyt duże. Czasami zatem rozważa się też tzw. nominanty, tj. zmienne, które mają jakiś optymalny zakres. Nie będziemy jednak komplikować sprawy.

Na potrzeby TMAI zmienne są standaryzowane, aby miały te sam rzędy wielkości i miana:

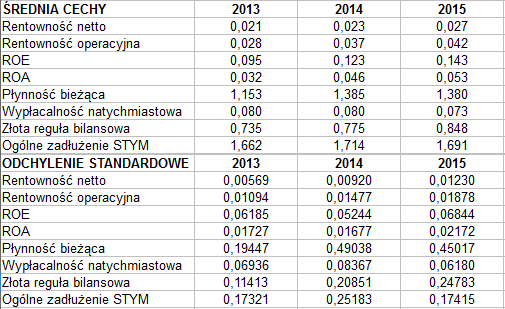
Jak widać, by uzyskać z_ij - czyli zestandaryzowany odpowiednik x_ij - odejmujemy od wyjściowej wartości średnią arytmetyczną zmiennej (tzn. średnią z wyników czterech spółek za dany rok) i dzielimy przez odchylenie standardowe tejże zmiennej (cechy). I tak dla trzech lat oraz dla wszystkich cech:

Mamy już ustandaryzowane zmienne, tzn. takie, że każda ma wartość średnią równą 0 oraz odchylenie standardowe równe 1. Zaznaczmy: cały czas mowa o średniej z czterech spółek, a nie np. o średniej dla jednej spółki z trzech lat.

Pora wyobrazić sobie przedsiębiorstwo wzorcowe. Spójrzmy na tabelkę:

Co widzimy? Najpierw w każdym roku wybraliśmy maksimum każdego ze wskaźników. Czyli np. wzorcowa rentowność netto za rok 2013 to 0,931 - taką wartość miała firma Tarczyński (wartość po standaryzacji - prawdziwa jej rentowność za ów okres to 2,7 proc.).

Następnie - w prawej tabeli - bierzemy dla każdej cechy jej maksimum z trzech lat. A zatem niezależnie od tego, czy będziemy rozważać rok 2013, 2014 czy 2015, to za każdym razem wyniki spółki z tego okresu porównywać będziemy z tym samym wzorcem, niezależnym od czasu. Ma to zapewne wady i zalety - ale jakoś trzeba się umówić. Alternatywą byłoby posiadanie w każdym roku osobnego wzorca. Można byłoby to jakoś uzasadnić - np. sugerując, że czasy się zmieniają i np. w roku 2014 kryterium powinno być inne niż w 2013. Z drugiej strony, utrudniałoby to nam analizowanie zmian finalnego TMAI w czasie. Na przykład w roku 2014 firma byłaby bliżej wzorca niż w 2013 - ale tylko dlatego, że wzorzec znacząco się osłabił.

A zatem mamy jeden wzorzec dla wszystkich lat. W każdym okresie żądamy zbliżania się do tego samego, ponadczasowego ideału - mówiąc uroczyście.

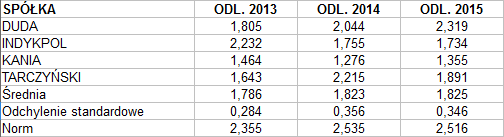
Jak liczymy odległość od wzorca? Można tu wykorzystać zwykłą metrykę euklidesową:

Przez z_oj rozumiemy kolejne wskaźniki przedsiębiorstwa wzorcowego. U nas m = 8, bo mamy 8 takich wskaźników. Wzór, który widzimy, przypomina trochę odchylenie standardowe. W pewnym sensie tak jest - sprawdzamy odchylenie spółki od ideału.

Spójrzmy:

Wydawałoby się, że to już wszystko, ale to wciąż jeszcze nie TMAI. Otóż teoria nakazuje, by TMAI mieścił się w obszarze [0, 1] i miał naturalną interpretację - tzn. taką, że im wyższy wynik, tym lepiej. Na razie mamy sytuację odwrotną - im wyższy wynik, tym gorzej, bo tym dalej jesteśmy od ideału.

Zauważmy jednak, że obliczyliśmy dla każdego roku średnią odległość spółki, a także odchylenie standardowe - i na koniec wielkość oznaczoną jako 'norm'. Nie bez powodu. Oto bowiemy finalny wzór:

Otóż tak wyliczony TMAI będzie spełniał żądane warunki. Naturalnie trzeba wiedzieć, czym jest 'norm'. Definicja wygląda tak:

Jest to więc suma średniej z uzyskanych odległości oraz podwojonego odchylenia standardowego tychże. Nie musimy stosować podwojenia, w miejsce liczby 2 mogłoby być inne naturalne k, ale to już niuans.

Oto końcowe rezultaty:

Próba jest mała - zarówno pod względem liczby spółek, jak i liczby badanych okresów. Pewne zjawiska można jednak zaobserwować. Na przykład TMAI dla Henryka Kani przyjmuje najlepsze wartości - i w jakiś sposób komponuje się to z rzeczywiście obserwowanym rozwojem tego przedsiębiorstwa (coraz wyższe obroty i marże).

Z kolei w PKM Duda było w ostatnich latach trochę czynników osłabienia - np. spadały przychody tudzież zyski EBIT i netto. W 2015 wartości ROE i ROA były wyraźnie słabsze niż rok i dwa lata wcześniej. 

Indykpol miał np. dość słaby rok 2013 (marża netto tylko 0,21 proc., płynność bieżąca 1,24 pkt, marża operacyjna 1,44 proc.) - ale potem sytuacja się poprawiła i TMAI też wzrósł.

W spółce Tarczyński rok 2014 przyniósł m.in. znaczącą obniżkę ROE i ROA, a także spadek płynności bieżącej, wypłacalności natychmiastowej i marży netto (choć np. marża operacyjna wzrosła z 3,86 proc. do 4,37 proc.).

Zauważmy, że w naszym modelu wszystkie wskaźniki mają takie samo znaczenie. Nie jest np. tak, że premiujemy rentowność operacyjną kosztem płynności bieżącej czy odwrotnie. Nie jest to jednak jedyne możliwe podejście. Przeciwnie, w praktyce często wyposaża się w zmienne w odpowiadające im wagi. Przyjmuje się następujące wzory:

Tak określony system wag uwzględnia zmienność danej cechy, premiując wskaźniki o największej zmienności jako najistotniejsze. Tę ostatnią wyraża V_j - tj. stosunek odchylenia standardowego do średniej. Pamiętajmy: chodzi o j-tą zmienną spośród m (czyli np. trzecią z ośmiu, u nas byłoby to ROE) oraz o średnią jej wartość dla badanych spółek (za dany rok).

W takim układzie modyfikujemy wzór odległości:

Reszta przebiega tak samo. Okazuje się jednak, że można dokonać znacznie poważniejszej zmiany w całej metodologii. W ślad za A. Rutkowską-Ziarko i M. Sochoniem można mianowicie zasugerować wykorzystanie metryki innej niż euklidesowa.

Jest to - patrząc czysto teoretycznie - rzecz dopuszczalna. Tak samo w życiu liczymy odległość na różne sposoby. Wyobraźmy sobie, że chcemy z jednego rogu basenu przedostać się do przeciwległego (tego "na skos"). Możemy przepłynąć po przekątnej (metryka euklidesowa) - albo obejść dwa boki. Euklidesowo będzie szybciej, ale być może nie umiemy pływać...?

Z różnych przyczyn metryka euklidesowa nie zawsze jest najlepsza. Nie miejsce tu, by wnikać w szczegóły, ale autorzy, których przytoczyliśmy, postulują wykorzystanie w TMAI tzw. odległości Mahalanobisa. Wprowadził ją w 1936 roku statystyk z Indii - P. C. Mahalanobis (w pracy 'On the generalized distance in statistics').

Wzór jest następujący:

Przez W_i rozumiemy wektor (wierszowy) wskaźników i-tej spółki (w ustalonym roku). Z kolei W_l to znany już wektor idealnego przedsiębiorstwa, wzorcowy. Ale uwaga: pojawia się jeszcze C, a nawet C^-1. Otóż C to macierz kowariancji wektora W_i za dany okres. Nie będziemy wnikać w szczegóły: w skrócie rzecz można, że macierz ta na przekątnej ma wariancje k-tej zmiennej wektora (k-tego wskaźnika), a poza przekątną każdy wyraz o indeksie kl to kowariancja k-tej i l-tej zmiennej. Na przykład kowariancja ROE i płynności bieżącej. Wzór na kowariancję dwóch wartości (ogólnie: dwóch zmiennych losowych X, Y) jest taki:

A zatem od średniego iloczynu odejmujemy iloczyn średnich. Znów chodzi tu o średnią wartość np. ROE w gronie badanych spółek za dany rok.

Finalny wzór TMAI i-tym roku jest taki:

Spółka najdalsza od wzorca będzie mieć TMAI w pobliżu zera, im zaś wyższa wartość, tym lepiej. Przy stosowaniu odległości Mahalanobisa nie trzeba standaryzować zmiennych.

Adam Witczak

BIBLIOGRAFIA:

A. Rutkowska-Ziarko, M. Sochoń, Wykorzystanie odległości Mahalanobisa do diagnozowania objawów kryzysu na przykładzie spółek branży budowlanej notowanych na GPW w Warszawie, w: Zastosowanie metod ilościowych w zarządzaniu ryzykiem działalności inwestycyjnej, red. A. S. Barczak, P. Tworek, Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013

A. Mastalerz-Kodzis, E. Pośpiech, Zastosowanie wybranych elementów analizy fundamentalnej do wyznaczania portfeli optymalnych, Uniwersytet Ekonomiczny w Katowicach
 
J. Jóźwiak, J. Podgórski, Statystyka od podstaw, Polskie Wydawnictwo Ekonomiczne 1998

A. Pieloch-Babiarz, Ocena atrakcyjności inwestycyjnej spółek giełdowych odpowiedzialnych społecznie, Zarządzanie i Finanse - Journal of Management and Finance, vol. 13, no. 1/2015

S. Bartosiewicz, M. Otorowski, Budowa i analiza TMAI dla spółek notowanych na Giełdzie Papierów Wartościowych

W. Tarczyński, Rynki kapitałowe - metody ilościowe, Agencja Wydawnicza "Placet" 1997