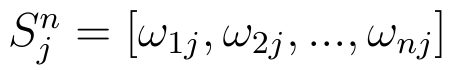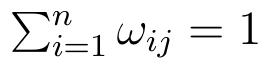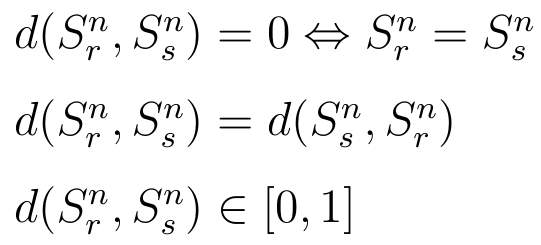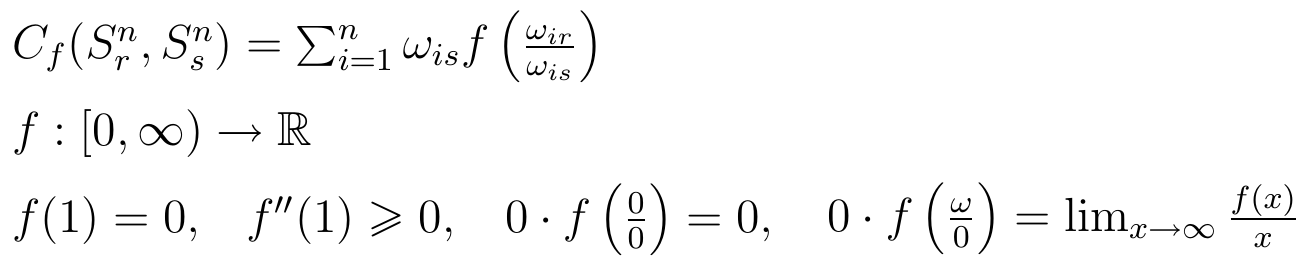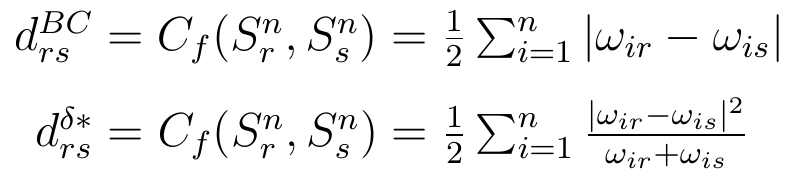Miary podobieństwa populacji

Załóżmy, że mamy dwie populacje. W teorii mogą to być bardzo dowolne struktury, ale dla ustalenia uwagi przyjmijmy, że chodzi o dwie zbiorowości ludzkie, np. społeczeństwa dwóch państw.

Możemy wybrać jakieś kryterium i sprawdzić, czy zbiorowości te są do siebie podobne ze względu na tę cechę. Taką cechą może być np. struktura wyznaniowa. Jeżeli w obu państwach ok. 3/4 ludności to muzułmanie i ok. 1/4 to chrześcijanie, wówczas uznamy te społeczeństwa za podobne (nawet jeśli konkretne odsetki trochę się od siebie różniły - i było to 73 vs 27 proc. oraz 76 vs 24 proc.).

Oczywiście może być i tak, że w jednym państwie 80 proc. mieszkańców to buddyści, 15 proc. to muzułmanie i 5 proc. to chrześcijanie, a w drugim 40 proc. wyznaje luteranizm, 35 proc. prawosławie i 25 proc. islam. Wówczas uznamy te społeczności za bardzo różne (pod względem religijnym).

Inny dobry przykład to struktura wiekowa ludności. Jeżeli w obu zbiorowościach ok. 25 proc. mieszkańców ma nie więcej niż 14 lat, ok. 65 proc. ma 15 - 64 lata i ok. 10 proc. to ludzie starsi - wówczas znów zauważymy podobieństwo.

Ale to wszystko oceny "na oko". Są dobre, dopóki porównujemy dwie, trzy zbiorowości, które są w dość wyraźny sposób podobne lub odmienne (parami). Kiedy populacji jest więcej i kiedy nie odstają od siebie w sposób ewidentny, sprawa się komplikuje. Chcemy mierzyć podobieństwo w jakiś ustalony, matematyczny, sensowny sposób. Czytelnik domyśla się z pewnością, że takich sposobów jest wiele. Żaden nie jest "obiektywny" czy "uniwersalnie prawdziwy". Innymi słowy, paradoks tkwi w tym, że dopiero funkcja mierząca podobieństwo... mówi nam, czym to podobieństwo jest. Naturalnie tak jest zawsze w statystyce, ekonometrii i innych działach matematyki. Z drugiej strony, staramy się te funkcje budować tak, by pasowały do naszych elementarnych intuicji.

Przejdźmy do rzeczy. W demografii i ekonomii często operuje się tzw. miarami dywergencji z klasy Csiszára (inaczej: f-dywergencjami). To pewna rodzina funkcji, zresztą bardzo rozległa, które mają określone cechy, dzięki którym dobrze sprawdzają się jako miary podobieństwa.

Zacznijmy od ustalenia podstawowych oznaczeń. Nasze populacje oznaczamy przez O_j, gdzie j = 1, ..., 2. To znaczy: mamy m zbiorowości (np. 6 państw). Każda populacja ma swój wektor wskaźników struktury:

W istocie elementy ω_ij to procentowe udziały (np. udział kolejno muzułmanów, chrześcijan i buddystów w j-tej populacji). Dlatego też możemy swobodnie przyjąć następujące ograniczenia (traktując procenty jako ułamki dziesiętne):

Samymi obiektami O_j nie będziemy się zbytnio zajmować: po prostu utożsamimy je z odpowiadającymi im wektorami struktur. Stąd też będziemy mówić: zbiorowość (populacja) S_rⁿ, S_sⁿ itd.

*

Od dobrej miary podobieństwa zwykle oczekuje się co najmniej trzech poniższych cech:

Innymi słowy, miara d pomiędzy populacjami S_rⁿ i S_sⁿ wynosi 0, gdy zbiorowości te mają identyczną strukturę ze względu na badaną cechę (co w rzeczywistym świecie zdarza się rzadko). Żąda się też, by miara (odległość) od jednej do drugiej populacji była... taka jak od drugiej do pierwszej. To naturalne, ale trzeba rzecz zadeklarować. Poza tym odległość ta nie powinna przekraczać liczby 1. Oczywiście mogłaby to być też liczba 100 (albo 200), ale liczba 1 jest najwygodniejsza.

Miara dywergencji z klasy Csiszára to każda miara C_f następującej postaci:

Jak widać, C_f jest zależna od funkcji f, przy czym zakładamy (poza tym, co zapisaliśmy w formule), że f jest różniczkowalna i wypukła.

Okazuje się, że wiele znanych metryk to f-dywergencje, np. metryka miejska czy tzw. odległość Hellingera. My zaprezentujemy dwa przykładowe narzędzia: odległość Braya-Curtisa d_rs^BS i unormowaną odległość trójkąta d_rs^*:

Wzór Braya-Curtisa jest bardzo prosty. Bierzemy i-tą (na początek pierwszą, na przykład odsetek muzułmanów - albo emerytów, zależnie od tego, jaką cechę badamy) wielkość w pierwszej populacji, odejmujemy od niej odpowiednią wielkość dla drugiej populacji, bierzemy moduł (wartość bezwzględną) i przechodzimy do drugiej wielkości (na przykład do odsetka buddystów). Postępujemy tak samo, dodajemy uzyskane wyniki, a sumę dzielimy przez 2.

Unormowana metryka trójkąta jest nieco bardziej skomplikowana, bo mamy tu dodawanie, odejmowanie, moduł, kwadrat i ułamek (a potem jeszcze sumowanie i podobnie jak poprzednio dzielenie przez 2), niemniej wzór nie jest bardzo ezoteryczny.

A teraz odrobina praktyki. Zajmiemy się grupami wiekowymi w sześciu (dobranych dość arbitralnie) państwach. Rozważać będziemy tylko trzy grupy: do 14 lat, od 15 do 64 lat - i od 65 lat wzwyż. Nie chodzi nam bowiem o szczegółowe badania (te przecież prowadzone są przez GUS i inne instytucje), a jedynie o szybkie zastosowanie wzorów na dość prostych danych.

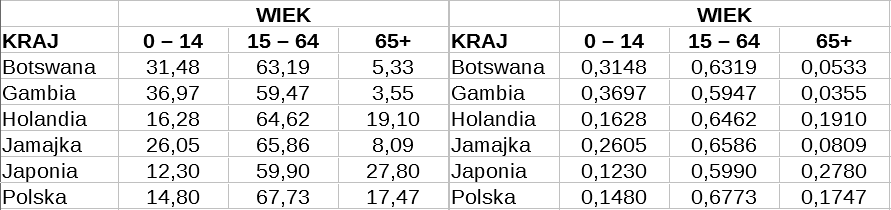
Spójrzmy na informacje dotyczące demografii Botswany, Gambii, Holandii, Jamajki, Japonii i Polski.

W pierwszej tabeli dane są w postaci procentowej (np. aż 27,8 proc. Japończyków to ludzie starzy, zaś aż 36,97 proc. Gambijczyków to dzieci). W drugiej mamy te same dane, ale wyrażone jako ułamki dziesiętne.

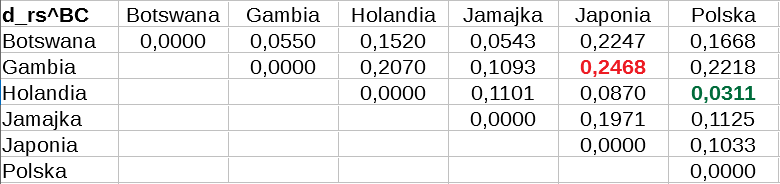
Druga tabela prezentuje odległości Braya-Curtisa pomiędzy wszystkimi wymienionymi państwami.

Z oczywistych względów na przekątnej mamy same zera (każdy kraj jest przecież identyczny sam ze sobą). Miejsca poniżej przekątnej są wypełnione tak samo jak te po drugiej stronie (jak pamiętamy, metryka Csiszára jest symetryczna), ale usunęliśmy te wyniki, żeby tabela była bardziej czytelna.

Botswana i Gambia, zgodnie z intuicją, okazują się bardzo podobne do siebie: obliczona wartość to 0,0550 pkt, bardzo bliska zeru. Ale jeszcze mniej różni Polskę i Holandię: dla tej pary rezultat to 0,0311 pkt - i jest to najniższa liczba w całej puli (pomijając wyniki zerowe). Druga skrajna para to Gambia i Japonia: tu mamy 0,2468 pkt (czyli ok. 0,25 pkt). To znaczy, że oba te państwa bardzo się różnią, jeżeli chodzi o strukturę ludności. W istocie trudno byłoby znaleźć obecnie na świecie parę krajów, która dałaby nam większy wynik w metryce Braya-Curtisa: albowiem Japonia uchodzi za jedno z "najstarszych" społeczeństw na Ziemi, zaś Gambia za prawie "najmłodsze".

Polska i Gambia też się mocno różnią (0,2218 pkt), podobnie np. Holandia i Gambia (0,2070 pkt). Jamajka jest z pewnością bardziej podobna do Polski (0,1125 pkt) niż do Japonii (0,1971 pkt), ale znacznie bardziej odmienna od nas niż Holandia. Możemy też wyliczyć wiele innych takich zależności - i to właśnie jest pożytek z opisanego narzędzia.

Dodajmy, że inna formuła dywergencji (np. odległość trójkąta albo Kullbaca-Leiblera) dałaby prawdopodobnie inne wyniki (inny ranking), choć można podejrzewać, że podstawowe i skrajne zależności pozostałyby takie same.

Adam Witczak


BIBLIOGRAFIA:

E. Wędrowska, M. Forkiewicz, "Wykorzystanie miar dywergencji Csiszara do oceny podobieństwa struktury ludności krajów regionu Morza Bałtyckiego", w: "Współczesne problemy demograficzne w dobie globalizacji - aspekty pozytywne i negatywne", seria "Studia Ekonomiczne", Zeszyty Naukowe Wydziałowe Uniwersytetu Ekonomicznego w Katowicach, Katowice 2011.

I. Csiszár, "Information-Type Measures of Difference of Probability Distributions and Indirect Observations", Studia Scientiarum Mathematicarum Hungarica, 2, 1967, 299-318.