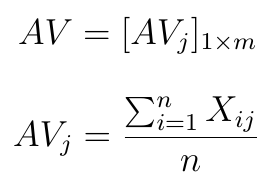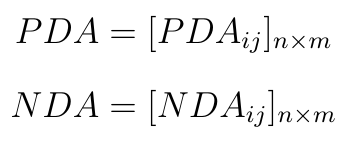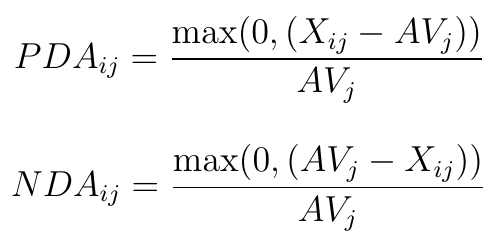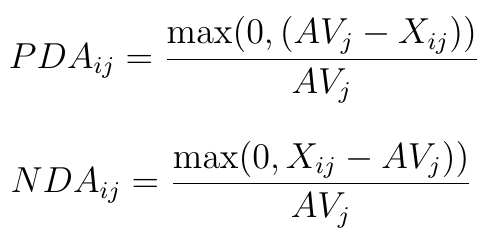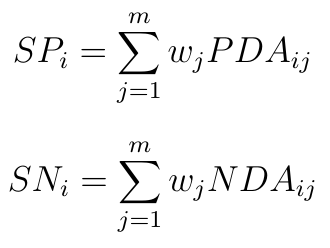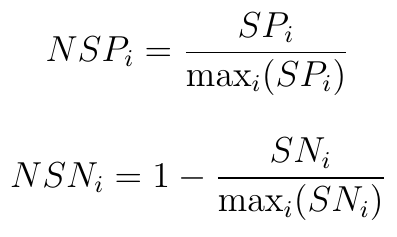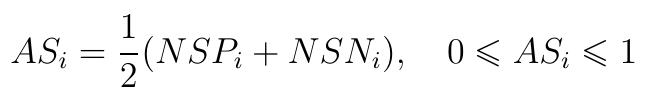EDAS - metoda wzorca przeciętnego

Omówimy dziś kolejną metodę wielokryterialną z klasy tych, w których istotą rozwiązania jest pomiar odległości pomiędzy badanymi scenariuszami a pewną alternatywą wzorcową, wygenerowaną sztucznie.

Zazwyczaj tym wzorcem odniesienia jest teoretyczny scenariusz najlepszy, względnie najgorszy (czasami oba). Taki scenariusz buduje się zwykle tak: ustalamy kryterium, w pierwszym kroku jest to oczywiście kryterium nr 1. Następnie przeglądamy wszystkie dostępne alternatywy i wybieramy najlepszą względem tego kryterium. Tę wartość zapamiętujemy i przechodzimy do kolejnego kryterium. W efekcie powstaje scenariusz który można kolokwialnie opisać tak: "dla każdego kryterium przyjmujemy najlepszy z dostępnych wyników" albo "bierzemy z każdej alternatywy to, co w niej najlepsze". Analogicznie rzecz wygląda przy szukaniu anty-wzorca, tylko że wtedy interesują nas najsłabsze wyniki.

Słów "alternatywa", "scenariusz" i "wariant" używamy zamiennie. Na naszym portalu często stosujemy metody MCDM w czasie analiz - i wówczas naszymi scenariuszami są spółki giełdowe, rozpatrywane pod kątem wskaźników finansowych.

Metoda EDAS polega na tym, że naszym wariantem odniesienia staje się scenariusz pośredni czy też przeciętny. Można to rozmaicie uzasadniać. Na przykład można myśleć, że każdy scenariusz wiąże się z określonymi kosztami. Gdybyśmy wygenerowali wzorzec oparty na maksymalizacji wartości kryteriów (jak to opisaliśmy wcześniej), to najbliższe mu scenariusze byłyby prawdopodobnie drogie. Warto więc zbalansować zagadnienie. Stąd też interesować będzie nas odległość do rozwiązania pośredniego, AV (average).

EDAS to zupełnie nowa metodologia. Technika została zaprezentowana w pracy M. K. Ghorabee, E. K. Zavadskasa, L. Olfata i Z. Turskisa zatytułowanej "Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS)", opublikowanej w 2015 na łamach pisma "Informatica". Większość oznaczeń bierzemy właśnie z tej pracy, natomiast przykład jest naszym własnym dziełem. Swoją drogą, przedsięwzięcie jest efektem kooperacji uczonych irańskich i litewskich.

*

Zaczyna się tak jak zwykle: mamy macierz decyzyjną, to znaczy n alternatyw i m kryteriów. Alternatywy indeksowane są literką i, kryteria literką j.

Oczywiście X_ij to wynik i-tej alternatywy w świetle j-tego kryterium, np. jeśli 4-ta alternatywa w badanej puli to spółka Famur, a 2-gie kryterium to płynność bieżąca, wtedy X_42 to płynność Famuru.

Teraz określamy rozwiązanie pośrednie. Jest to wektor jednowierszowy o m kolumnach, tzn. dla każdego kryterium mamy w nim wartość średnią. Stosuje się tu najzwyklejszą średnią arytmetyczną.

Na razie nie mówiliśmy nic o charakterze poszczególnych kryteriów. Otóż mogą to być albo stymulanty (beneficial), albo destymulanty (non-beneficial). Co do tych pierwszych, to za dobre uznaje się takie wyniki, które są duże (im liczba większa, tym lepiej). Na przykład rentowność netto w spółce giełdowej zwykle jest takim kryterium. Te drugie są tym lepsze, im niższe. Na przykład zadłużenie może być tak postrzegane (choć to akurat duże uproszczenie).

Obliczamy dla każdej spółki macierze PDA (pozytywny dystans od rozwiązania średniego) i NDA (dystans negatywny). Ogólnie wyglądają one tak:

Pojawia się pytanie o to, jak obliczyć odpowiednie wyrazy. Otóż dla kryteriów typu stymulantowego wygląda to tak:

Jak łatwo zauważyć, jeśli PDA_ij jest większe od zera (czyli X_ij - AV_j > 0), to NDA_ij = 0 (gdyż wtedy AV_j - X_ij < 0).

Dla destymulant liczymy jak poniżej:

Kryteria mogą mieć różne wagi (które powinny się sumować do 1). To, jak te wagi dobrać, to osobne zagadnienie, również żywo dyskutowane wśród uczonych badających metody MCDM. Tu nie będziemy się tym zajmować. Wagi mogą być równe sobie (wtedy nie mają znaczenia), mogą być ustalone "na oko" lub obliczone przy pomocy pewnych metod statystycznych (lub mieszanych, łączących matematykę z subiektywnymi ocenami ekspertów).

W kolejnym kroku obliczamy zważone sumy PDA i NDA dla poszczególnych scenariuszy (w_j to waga j-tego kryterium):

Następny ruch to normalizacja uzyskanych wartości SP i SN. Chodzi o to, by były one ze sobą porównywalne, w tej samej skali.

Teraz prezentujemy formułę, według której oblicza się tzw. Appraisal Score (AS) dla każdej alternatywy:

Ostatni krok to uszeregowanie wartości AS_i w porządku malejącym (decreasing). Najlepsza spółka ma najwyższy wynik, najgorsza - najniższy.

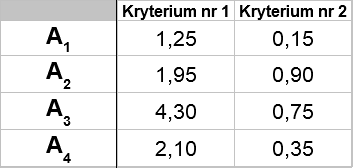
Wyobraźmy sobie następujący przykład. Mamy cztery alternatywy i dwa kryteria. Kryterium nr 1 to stymulanta i ma wagę 3/4, kryterium nr 2 to destymulanta z wagą 1/4.

Konkretne liczby wyglądają tak:

Trzeba wyliczyć najpierw współrzędne scenariusza pośredniego:

AV₁ = (1,25 + 1,95 + 4,30 + 2,10) / 4 = 2,40

AV₂ = (0,15 + 0,90 + 0,75 + 0,35) / 4 = 0,5375

Kolejny krok to wyliczenie odpowiednich odległości:

- Dla A₁:

PDA₁₁ = 0; NDA₁₁ = (2,40 - 1,25) / 2,40 = 0,48 (niektóre wartości będziemy podawać w wersji przybliżonej)

PDA₁₂ = (0,5375 - 0,15) / 0,5375 = 0,72; NDA₁₂ = 0

- Dla A₂:

PDA₂₁ = 0; NDA₂₁ = (2,40 - 1,95) / 2,40 = 0,1875.

PDA₂₂ = 0; NDA₂₂ = (0,90 - 0,5375) / 0,5375 = 0,674.

- Dla A₃:

PDA₃₁ = (4,30 - 2,40) / 2,40 = 0,79; NDA₃₁ = 0

PDA₃₂ = 0; NDA₃₂ = (0,75 - 0,5375) / 0,5375 = 0,395.

- Dla A₄:

PDA₄₁ = 0; NDA₄₁ = (2,40 - 2,10) / 2,40 = 0,125.

PDA₄₂ = (0,5375 - 0,35) / 0,5375 = 0,349; NDA₄₂ = 0.

Teraz obliczamy SP i SN:

- Dla A₁:

SP₁ = 3/4 * 0 + 1/4 * 0,72 = 0,18.
SN₁ = 3/4 * 0,48 + 1/4 * 0 = 0,36.

- Dla A₂:

SP₂ = 3/4 * 0 + 1/4 * 0 = 0.
SN₂ = 3/4 * 0,1875 + 1/4 * 0,67 = 0,1406 + 0,1675 = 0,308.

- Dla A_3:

SP₃ = 3/4 * 0,79 + 1/4 * 0 = 0,5925.
SN₃ = 3/4 * 0 + 1/4 * 0,395 = 0,098.

- Dla A_4:

SP₄ = 3/4 * 0 + 1/4 * 0,349 = 0,087.
SN₄ = 3/4 * 0,125 + 1/4 * 0 = 0,094.

*

Teraz normalizujemy wartości:

NSP₁ = 0,18 / 0,5925 = 0,304.
NSN₁ = 1 - 0,36 / 0,36 = 0.

NSP₂ = 0.
NSN₂ = 1 - 0,308 / 0,36 = 0,144.

NSP₃ = 0,5925 / 0,5925 = 1.
NSN₃ = 1 - 0,098 / 0,36 = 0,728.

NSP₄ = 0,087 / 0,5925 = 0,147.
NSP₄ = 1 - 0,094 / 0,36 = 0,739.

*

Obliczamy wartości AS:

AS₁ = 1/2 (0,304 + 0) = 0,152.
AS₂ = 1/2 (0 + 0,144) = 0,072.
AS₃ = 1/2 (1 + 0,728) = 0,864.
AS₄ = 1/2 (0,147 + 0,739) = 0.443.

Szeregujemy te wartości malejąco i otrzymujemy następujący ranking alternatyw:

A₃ - 0,864

A₄ - 0,443

A₁ - 0,152

A₂ - 0,072

To oznacza, że w świetle EDAS najlepszy jest scenariusz nr 3. Czy można to sobie jakoś zracjonalizować? Cóż, na pewno pierwsze kryterium jest tam zrealizowane bardzo wysoko: na poziomie 4,30 pkt. To w pewnym sensie "przebija" słabość drugiego kryterium (aż 0,75 pkt, podczas gdy to destymulanta). W scenariuszu nr 4, który zajął miejsce nr 2, drugie kryterium wypada lepiej, ale pierwsze znacznie gorzej. Scenariusz A₁ ma bardzo niski, więc bardzo dobry, poziom kryterium drugiego, lecz najgorszy w świetle kryterium pierwszego. Wreszcie scenariusz A₂ ma niespecjalnie przebojowy wynik na pierwszym kryterium i bardzo słaby na drugim (najgorszy).

Ostatecznie jednak takie metody jak EDAS powstają właśnie po to, byśmy mogli uniknąć tego rodzaju niejasnych rozważań: chodzi o to, by w syntetyczny sposób badać wiele (dziesiątki? setki?) alternatyw, które zresztą mogą się od siebie różnić dość nieznacznie. Algorytm oczyszcza nam percepcję.

Adam Witczak

BIBLIOGRAFIA:

M. K. Ghorabee, E. K. Zavadskas, L. Olfat i Z. Turskis, "Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS)", INFORMATICA, 2015, Vol. 26, No. 3, 435–451

E. K. Zavadskas, F. Cavallaro, V. Podvezko, I. Ubarte, A. Kaklauskas, "MCDM Assessment of a Healthy and Safe Built Environment According to Sustainable Development Principles: A Practical Neighborhood Approach in Vilnius", Sustainability 2017, 9, 702.

A. Aggarwal, Ch. Choudhary, D. Mehrotra, Evaluation of smartphones in Indian market using EDAS, International Conference on Computational Intelligence and Data Science (ICCIDS 2018).