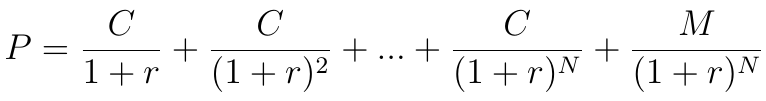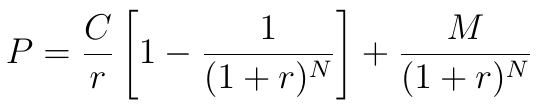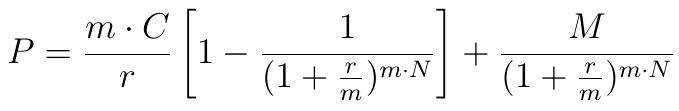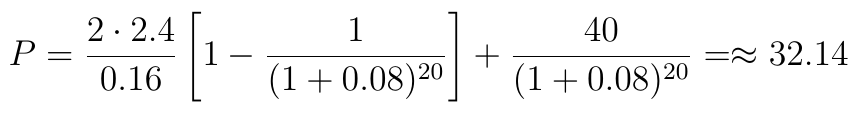Wycena obligacji o stałych odsetkach

W praktycznych zagadnieniach inwestycyjnych zazwyczaj oblicza się stopę zwrotu z obligacji, zwłaszcza na rynku wtórnym. Jest to tzw. yield to maturity (YTM), zwana też czasami stopą dyskontową (termin ten bywa używany też w innych kontekstach). Obserwatorzy rynku giełdowego i walutowego znają tę standardową zasadę: im wyższa rentowność, tym niższa cena.

Można powiedzieć, że YTM to stopa przy której wartość obecna przyszłych przepływów pieniężnych generowanych przez obligację (a te przepływy to odsetki i wykup nominału przez emitenta) równa się cenie zapłaconej za obligację przez jej nabywcę.

Sytuację można jednak odwrócić i zainteresować się tym, jaka powinna być cena obligacji przy ustalonej stopie YTM. Zajmiemy się przypadkiem obligacji o stałym oprocentowaniu. Przyjmijmy najpierw, że stałe odsetki wypłacane są w zgodzie z okresem stopy YTM, którą tu będziemy oznaczać przez r. Bazowo możemy tu przyjąć, że okres ten to po prostu rok.

Niech do tego M oznacza wartość nominalną papieru, zaś N rok wykupu (np. N = 10, jeśli to papier 10-letni). Roczny wpływ z odsetek to C. Cenę obligacji - taką, na jaką możemy się zgodzić - oznaczymy przez P. Mamy wtedy wzór:

Wynika on z tego, że dyskontujemy roczne wpływy, tak więc w każdym składniku sumy dzielimy C przez (1+r) w odpowiedniej potędze, a do tego w roku N-tym emitent wykupuje nominał, zatem kwota M też jest dyskontowana.

Można przetworzyć wzór i napisać:

Może się też zdarzyć, że otrzymujemy odsetki w innej częstotliwości niż ta sugerowana przez stopę r, tzn. m razy w okresie tej stopy (m razy w roku, jeśli jest ona roczna). Wówczas zamiast r weźmiemy w naszej formule r/m, zamiast N natomiast n*m. Efekt jest taki:

Wyobraźmy sobie teraz, że rozważamy obligację 10-letnią o nominalnej wartości 40 tys. zł. Jej nominalna roczna stopa procentowa to 12 proc., a YTM = r to 16 proc. Odsetki wypłacane są dwa razy w roku. Tak więc, skoro roczna stopa to 12 proc., wówczas pojedyncza wypłata to 6 proc. z 40 (tys.), tj. 2.4 (tys.). Wielkość m*n = 20, zaś r/m to 0.16/2 = 0.08. Podstawiamy dane do wzoru i otrzymujemy:

A zatem nominał obligacji to 40 (tys. zł), ale cena rynkowa, jaką powinniśmy dać przy ustalonej, 16-procentowej stopie r, to tylko 32,14 (tys. zł). Właściwa cena papieru jest zatem niższa od nominalnej, bo r jest większe od stopy kuponu.

Adam Witczak

BIBLIOGRAFIA:

M. Dobija, E. Smaga, "Podstawy matematyki finansowej i ubezpieczeniowej", PWN 1995.

M. Podgórska, J. Klimkowska, "Matematyka finansowa", PWN 2005.