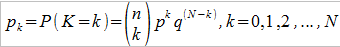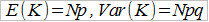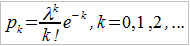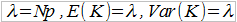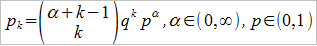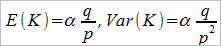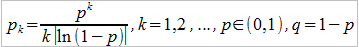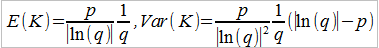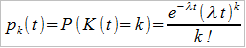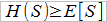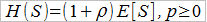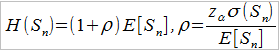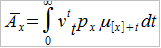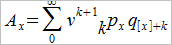Aktuarialne podstawy non-life

Matematyka ubezpieczeniowa czy też aktuarialna dzielona jest zazwyczaj na dwie dyscypliny: jedna zajmuje się ubezpieczeniami na życie, druga natomiast – wszelkimi innymi, w polskiej terminologii określanymi jako majątkowe i (pozostałe) osobowe. Anglojęzyczne określenia to po prostu life i non-life (insurances).

Formalnie rzecz biorąc, według ustawy o działalności ubezpieczeniowej mamy Dział I – ubezpieczenia na życie – oraz Dział II, czyli pozostałe ubezpieczenia osobowe i majątkowe. Do Działu I zalicza się ubezpieczenia: 1) na życie, 2) posagowe, zaopatrzenia dzieci, 3) na życie, związane z funduszem inwestycyjnym, 4) rentowe, 5) wypadkowe i chorobowe – ale jako uzupełnienie grup 1) – 4).

Dział II to np. ubezpieczenia pojazdów (różnego rodzaju), chorobowe i wypadkowe (ale – por. poprzedni akapit – nie jako uzupełnienie ubezpieczeń life), na okoliczność katastrof naturalnych (powodzie, pożary etc.), na okoliczność niewypłacalności kredytowej etc. Ogółem ustawa podaje aż 18 grup w Dziale II.

W obu dyscyplinach podstawowe problemy to: 1) modelowanie i obliczanie prawdopodobieństwa zajścia szkody (w tym zgonu); 2) teoria ruiny (a więc analizowanie potencjalnych sytuacji, w których stan kapitału firmy ubezpieczeniowej zejdzie poniżej zera i braknie środków na wypłatę odszkodowań, przynajmniej w oparciu o standardowe źródła dochodów); 3) rozkład wartości indywidualnej szkody / roszczenia; 4) kalkulacja składki, jaką powinien wpłacić lub wpłacać ubezpieczony; 5) reasekuracja, czyli wzajemne ubezpieczenie się zakładów ubezpieczeniowych.

W dalszej części tekstu przedstawimy podstawowe wzory stosowane w matematyce aktuarialnej, w tej części tekstu skupiając się głównie na obszarze non-life.

W ubezpieczeniach drugiego rodzaju, majątkowych i osobowych, liczbę szkód na ogół modeluje się rozkładami dyskretnymi: - dwumianowym; - Poissona; - ujemnym dwumianowym; - logarytmicznym.

Zasadniczo będzie nas interesować portfel o charakterze jednorodnym. To jest zbiór N polis, które są do siebie w pewnym sensie podobne – to znaczy uznajemy, że ryzyko wystąpienia szkody jest w przypadku każdej z tych polis mniej więcej takie samo. Założenie to wynika z faktu, że mówimy np. o możliwości pożaru, która dotyczy podobnych do siebie (ze względu na konstrukcję, wartość, wielkość) budynków w określonym obszarze miasta.

Zbiór portfeli tworzy blok, w którym nadal istnieje pewna cecha wspólna, ale rozumiana dużo szerzej. Innymi słowy, możemy mieć blok ubezpieczeń od np. pożaru, podzielony na portfele wyznaczone dla domów jednorodzinnych, hipermarketów, wieżowców, budynków drewnianych itd.

Przejdźmy jednak do matematyki. Zakładamy, że p to prawdopodobieństwo wystąpienia pojedynczej szkody, q to 1 – p i jest to prawdopodobieństwo, że szkoda nie wystąpi (dom się nie zapali). Wówczas następujący wzór (rozkład dwumianowy) opisuje prawdopodobieństwo wystąpienia k szkód w ciągu roku w portfelu:

Średnią wartością szkód (przewidywaną) będzie wartość oczekiwana dla tego rozkładu, a do tego możemy też obliczyć wariancję:

Przy portfelach o dużej liczbie ryzyk, z których każde jest obarczone niewielkim prawdopodobieństwem, często stosuje się rozkład Poissona i wtedy:

Przy czym:

Jeśli wariancja przekracza średnią, to stosuje się rozkład ujemny dwumianowy, w którym p to znów prawdopodobieństwo pojedynczej szkody, zaś pk to prawdopodobieństwo, że po k sytuacjach bez szkody wystąpi szkoda o numerze α:

Wówczas mamy:

Czasami przyjmuje się też rozkład logarytmiczny:

Zagadnienie można skomplikować, biorąc pod uwagę czynnik czasu. Otóż chodzi o to, że szkody mogą pojawiać się z określoną (na podstawie obserwacji) częstotliwością. Na przykład może być tak, że w danym miesiącu zwykle – na przestrzeni minionych lat – pożar lub powódź dotykały przeciętnie pewną liczbę domów. Jeśli częstotliwość jest stała (określona jako λ), to prawdopodobieństwo, że w czasie t wystąpiło k szkód, wyliczamy z wzoru na proces Poissona:

Sprawa może się skomplikować, mianowicie intensywność może w jakiś sposób zależeć od czasu, a może w ogóle przybrać jeszcze inny charakter – co ostatecznie prowadzi do tzw. mieszanego rozkładu Poissona, o czym jednak nie będziemy tu mówić.

Wspomnimy natomiast pokrótce o podstawach kwestii wyliczania składki w przypadku ubezpieczeń non life. Otóż składka jest to oczywiście kwota, którą powinni wpłacić ubezpieczeni – i powinna być taka, aby zakład był w stanie wypłacać odszkodowania (a w praktyce także pokrywać koszty swej działalności itd.). Chodzi o to, że roszczenia w danym portfelu winny być rekompensowane przez wpłacone z góry składki.

Jeśli S to wielkość odszkodowania w portfelu (a ściślej: zmienna losowa opisująca tę wielkość), to na początek można uznać, że składką będzie po prostu wartość oczekiwana tej zmiennej. Taką składkę określa się jako składkę netto, ale okazuje się, że (przy niezależnych, jednakowo rozłożonych ryzykach w portfelu – i korzystając z Prawa Wielkich Liczb) przy takim podejściu do sprawy prawdopodobieństwo, iż suma wypłat przekroczy zebrane składki – zmierza do 1.

W praktyce więc – i to nie z powodu kosztów działania zakładu ubezpieczeniowego – żąda się, by:

Przez H(S) rozumiemy sumaryczną wysokość składki (to, co wpłacić powinni wszyscy ubezpieczeni razem) i jest ona oczywiście w pewien sposób zależna od S. Jak można się domyślić, wszystko rozbija się o wyliczenie tzw. narzutu bezpieczeństwa, co daje wzór:

Ujmując rzecz jeszcze inaczej: można postawić sobie pytanie o to, jaka winna być wielkość składki, aby prawdopodobieństwo niewypłacalności (które w praktyce, przy skończonym portfelu, zawsze będzie dodatnie) było małe, równe określonej liczbie α. Liczbę tę można rozumieć jako kwantyl rzędu α rozkładu zmiennej S. Idąc tym tropem wyprowadza się wzory na składki odchylenia standardowego i wariancji. Spójrzmy dla ogólnego rozeznania na pierwszą z nich.

Zakładając, że S_n to suma n szkód X_i, rozkładu każdej z tych szkód nie znamy, a w portfelu jest ich przynajmniej 30, możemy przyjąć:

Wypada dodać, że z_α to kwantyl rzędu α zmiennej losowej Z, ta zaś ma rozkład normalny ze średnią 0 i wariancją 1 (por. różne formy Centralnego Twierdzenia Granicznego).

W ubezpieczeniach na życie (life) rozważa się rozmaite ich wersje, m.in. ubezpieczenia na całe życie, terminowe, czyste na dożycie, na dożycie, odroczone na całe życie (te wszystkie płatne są w chwili śmierci). Są też ubezpieczenia różnego rodzaju płatne na koniec roku lub podokresu śmierci. Tak naprawdę te pierwsze mają charakter raczej teoretyczny i rozpatruje się je często w modelu ciągłym, licząc całki tam, gdzie w praktyce mielibyśmy raczej szeregi (czyli wartości dyskretne).

Oblicza się zarówno jednorazową składkę netto, jak i obecną wartość wypłaty z ubezpieczenia. Duże znaczenie mają tu zaczerpnięte z klasycznej matematyki finansowej wzory na różnego rodzaju renty, które jednak zostają tu wzbogacone czynnikami związanymi z prawdopodobieństwem. Istotny jest bowiem rozkład przyszłego czasu życia, czyli np. prawdopodobieństwo tego, że aktualny x-latek przeżyje jeszcze określoną liczbę lat. Tenże rozkład opiera się albo na empirycznie budowanych tablicach trwania życia, albo na modelach teoretycznych. Te drugie służą raczej do książkowych przykładów, zakłada się w nich, że rozkład przyszłego czasu życia jest dany jakimś wzorem (prawa de Moivre'a, Gompertza, Makehama etc.). Na przykład zakłada się, że natężenie zgonów ma charakter wykładniczy (z odpowiednimi modyfikacjami).

Dla przykładu możemy przedstawić wzór na jednorazową składkę netto ubezpieczenia na całe życie, które gwarantuje wypłatę sumy 1 w chwili zgonu danej osoby:

Przy czym μ_[x]+t to funkcja określająca natężenie zgonów (intensywność śmiertelności) x-latka w chwili t, _tp_x to prawdopodobieństwo, że x-latek przeżyje jeszcze przynajmniej t lat, zaś v^t to funkcja dyskonta, definiowana jako e^-δt, gdzie δ to natężenie oprocentowania, tj. ln(1+i), i to stopa procentowa.

 W bliższej realiom wersji dyskretnej ten sam wzór wygląda tak:

Przy czym q_[x]+k to prawdopodobieństwo, że x-latek umrze w ciągu roku po uprzednim przeżyciu co najmniej k lat.

W matematyce ubezpieczeń życiowych, jak przed chwilą zauważyliśmy, stosuje się ogromną liczbę bardzo specyficznych oznaczeń, które mogą być trochę deprymujące dla początkującego adepta. Pojawia się sporo łacińskich i greckich liter, nawiasów i indeksów. Na przykład _t|up_x to prawdopodobieństwo, że osobna mająca obecnie x lat przeżyje jeszcze t lat, ale później umrze w ciągu następnych u lat. Istnieją też liczne oznaczenia na różne rodzaje rent.

To, co powyżej pokazaliśmy, to zupełny wstęp, ledwie pobieżny zarys nie tyle nawet autentycznej pracy analityków pracujących dla zakładów ubezpieczeniowych – ile podstawowego kursu matematyki ubezpieczeń non life (o life nie wspominając). Takie kursy, podobnie jak wykłady z ubezpieczeń życiowych, są prowadzone przede wszystkim na kierunkach matematycznych oraz ekonomicznych. Na tych pierwszych podstawowy kurs skupia się niemal wyłącznie na teoretycznych aspektach matematycznych – i de facto jest swego rodzaju rozszerzeniem i uszczegółowieniem rachunku prawdopodobieństwa, przynajmniej z matematycznego punktu widzenia. O aspektach prawnych, ekonomicznych, zwyczajowych etc. mówi się niewiele albo wcale. Ma to jednak pewną zaletę.

Otóż egzamin aktuarialny, zdawany przez Komisją Nadzoru Finansowego (podobnie jak np. egzamin na maklera), jest egzaminem czysto matematycznym (w odróżnieniu np. od testu dla brokerów ubezpieczeniowych). Ustawa wyjaśnia, że "aktuariuszem jest osoba fizyczna wykonująca czynności w zakresie matematyki ubezpieczeniowej, finansowej i statystyki, wpisana do rejestru aktuariuszy". Tenże aktuariusz, jak czytamy, zajmuje się: ustalaniem wartości rezerw techniczno-ubezpieczeniowych, kontrolowaniem aktywów stanowiących pokrycie tych rezerw, wyliczaniem marginesu wypłacalności, sporządzaniem rocznego raportu o stanie portfela ubezpieczeń i ustalaniem wartości składników zaliczanych do środków własnych.

Egzamin składa się z czterech części, przy czym matematyka ubezpieczeń majątkowych i osobowych jest tylko jedną z nich. Poza tym mamy jeszcze ubezpieczenia życiowe, matematykę finansową (z takimi tematami jak kapitalizacja złożona, wycena opcji i innych instrumentów, drzewa decyzyjne etc.) oraz ogólnie rachunek prawdopodobieństwa i statystykę. Zadania wymagają szybkich obliczeń, odpowiedzi wybiera się z czterech proponowanych (w dość podchwytliwy sposób, przewidujący potencjalne błędy), a za błędne odpowiedzi przyznaje się punkty ujemne. Miejmy jednak nadzieję, że nie zniechęci to młodych adeptów matematyki czy nawet ekonomii. Powinni zresztą wiedzieć jeszcze, że warunkiem bycia wpisanym w poczet aktuariuszy jest, prócz niekaralności, wyższego wykształcenia czy zdanych egzaminów, także wykonywanie dwuletniej praktyki pod kierunkiem innego aktuariusza.

Bibliografia:

P. Kowalczyk, E. Poprawa, W. Ronka-Chmielowiec, Metody aktuarialne, PWN 2013

W. Otto, Ubezpieczenia majątkowe, WNT 2004

R. Kulik, R. Szekli, Matematyka ubezpieczeń majątkowych, skrypt (Uniwersytet Wrocławski)

B. Błaszczyszyn, T. Rolski, Podstawy matematyki ubezpieczeń na życie, WNT 2004

Zarządzanie ryzykiem w ubezpieczeniach, pod red. W. Ronki-Chmielowiec, Wydawnictwo Akademii Ekonomicznej we Wrocławiu 2000.