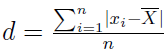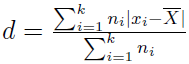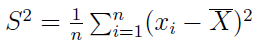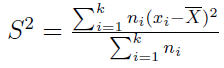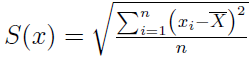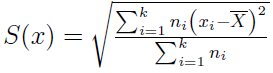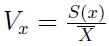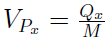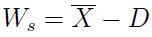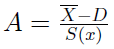Miary zmienności i asymetrii

Przedstawimy w poniższym artykule kilka podstawowych narzędzi, przy pomocy których w statystyce opisowej charakteryzuje się zbiorowość - tj. pewną kolekcję danych.

Oczywiście zawsze możemy zacząć od sprawdzenia średniej arytmetycznej, a także dominanty (wartości występującej najczęściej) czy mediany (jest to taka wartość, że połowa danych jest nie mniejsza od niej - lub też nie większa, co na jedno wychodzi).

Okazuje się jednak, że to nie wystarczy - bowiem możliwa jest sytuacja, w której dwie zbiorowości mają podobne lub nawet identyczne wartości średniej, mediany i dominanty, a pomimo tego różnią się na inne sposoby.

Otóż możemy w pierwszym kroku obliczyć odchylenie przeciętne - czyli średnią arytmetyczną z wartości bezwzględnych odchylenia od średniej. Istotne jest właśnie to, by brać moduły (wartości bezwzględne), aby uniknąć znoszenia się odchyleń dodatnich i ujemnych. Tak wygląda wzór dla szeregu szczegółowego:

Co to znaczy - szereg szczegółowy? Otóż jest to po prostu lista wszystkich zebranych wartości, nawet jeśli niektóre powtarzają się wiele razy. Na przykład: 1, 1, 2, 4, 4, 4, 4, 5, 5, 5, 7, 7, 11, 13.

W praktyce zwykle dzielimy szereg na klasy - do każdej z nich wstawiając wszystkie dane o jednakowej wartości. W powyższym przykładzie moglibyśmy więc wyróżnić siedem klas - np. dla liczby 1 (dwa elementy), dla liczby 2 (jeden element) czy dla liczby 4 (cztery elementy).

W takiej sytuacji powyższy wzór przybiera postać:

Przez k rozumiemy liczbę klas, a przez n_i - liczebność danej klasy.

Można też wyobrazić sobie, że klasy obejmują pewne przedziały domknięte - np. od 1 do 4, od 5 do 7 itd. W takiej sytuacji w każdym przedziale można wyznaczyć środek (średnią arytmetyczną dwóch wartości skrajnych), który oznaczymy przez x_i z kropką u góry. Wtedy wzór na odchylenie przeciętne wygląda tak:

Im wyższa wartość odchylenia przeciętnego w danej zbiorowości, tym gorzej średnia arytmetyczna oddaje jej strukturę. Wkrótce zobaczymy to na przykładach.

Kolejne narzędzie to wariancja. Jest to średnia arytmetyczna z kwadratów odchyleń poszczególnych wartości od średniej arytmetycznej wyliczonej dla całej populacji. Formuła wygląda tak:

- dla szeregu szczegółowego

- dla szeregu punktowo rozdzielczego:

Dla wersji przedziałowo rozdzielczej wzór będzie taki sam jak dla wersji punktowej - ale oczywiście będziemy brać pod uwagę środki przedziałów, podobnie jak przy odchyleniu przeciętnym.

Im bardziej zróżnicowana populacja, tym wyższą wartość przyjmuje wariancja. Można z niej też wyciągnąć pierwiastek, by otrzymać odchylenie standardowe:

Wyliczona wielkość informuje w pewien sposób o przeciętnym odchyleniu danych od średniej arytmetycznej. Można wykazać, że wartość odchylenia standardowego jest wyższa niż odchylenia przeciętnego. Czyli d < S.

Dodanie lub odjęcie do każdej z wartości w szeregu danych tej samej liczby ("przesunięcie" szeregu o pewną liczbę) nie zmienia ani odchylenia przeciętnego, ani standardowego. Z kolei przemnożenie wszystkich wartości przez tę samą liczbę a > 0 powoduje analogiczne powiększenie lub pomniejszenie odchyleń.

Warto pamiętać, że zarówno odchylenie standardowe jak i przeciętne są mianowane w jednostkach, w których wyrażono wartości szeregu danych - np. w zł czy kg. Zależą też od przyjętej skali. Nie wolno zatem porównywać odchyleń dla populacji przedstawionych w różnych skalach i jednostkach - np. gdybyśmy z jednej strony mieli przychody polskiej korporacji z 10 lat wyrażone w tysiącach złotych, a z drugiej - przychody firmy amerykańskiej za ten sam okres, ale w milionach dolarów jako podstawowej jednostce.

Ten mankament da się jednak obejść, możemy bowiem skorzystać z tzw. klasycznego współczynnika zmienności:

Jak widać, rzecz polega na tym, by podzielić odchylenie standardowe przez średnią arytmetyczną. Wartość współczynnika można przedstawiać w procentach - i często się to robi. Wówczas zwyczajowo przyjmuje się, że jeśli wynosi od zera do 20 proc., to zróżnicowanie badanej cechy jest w zbiorowości nader słabe, a jeśli wynik to więcej niż 80 proc. - wówczas jest ono ekstremalnie wysokie. Oczywiście wartość z powodzeniem może być wyższa niż 100 proc. Inna rzecz, że wtedy z pewnością nie ma sensu stosowanie średniej arytmetycznej jako narzędzia charakteryzującego zbiór.

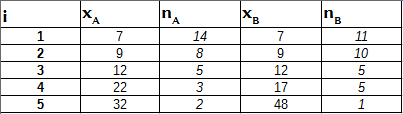
Czas na przykład. Rozważmy dwie populacje:

W kolumnach x_A i x__B wypisane są wartości badanej cechy, kolumny n_A i n_B mówią nam ile było przypadków danej wartości.

Populacje te dzielą się na tyle samo klas (mianowicie 5), jeśli przedstawimy je jako szeregi punktowo rozdzielcze. Obie mają po 32 elementy. W obu zestawach dominanta jest taka sama - wynosi 7 (w populacji A liczba 7 powtarza się 14 razy, w populacji B to 11 przypadków, wszystkie inne liczby pojawiają się rzadziej niż siódemka).

W obu populacjach średnia arytmetyczna, jak się okazuje, wynosi tyle samo, mianowicie 360 / 32 = 11,25. Mediana również jest taka sama, równa 9.

Odchylenie przeciętne w pierwszej populacji wynosi 4,84 - natomiast w drugiej jest ono niższe, osiąga wartość zbliżoną do 4,33.

W populacji A wariancja to 47 - natomiast w drugim zestawie to 55,25. Odchylenia standardowe wynoszą odpowiednio 6,85 i 7,43. Są one większe od odpowiadających im odchyleń przeciętnych, jak można się było spodziewać ze względu na ogólną prawidłowość. Z drugiej strony, tym razem w populacji B uzyskana miara jest wyższa niż w A.

Współczynnik zmienności dla populacji A to ok. 0,6 (czyli 60 proc.), w populacji B mamy 0,66 (66 proc.). W obu przypadkach zróżnicowanie cechy w zbiorowościach można uznać za bardzo (choć nie skrajnie) silne.

Idźmy dalej w rozważania teoretyczne. Przedstawiamy formułę odchylenia ćwiartkowego:

Przez Q₁ i Q₃ rozumiemy odpowiednio pierwszy i trzeci kwartyl. Pierwszy kwartyl to taka liczba, że 1/4 danych przyjmuje wartości nie większe od niej, analogicznie rozumujemy w przypadku trzeciego (wtedy oczywiście rozważamy 3/4 danych).

Odchylenie ćwiartkowe mierzy zmienność połowy najbardziej typowych elementów populacji. Przypadki skrajne są natomiast pomijane, co jest korzystne, jeżeli zbiorowość jest zaburzana przez niewielką liczbę wartości bardzo małych lub bardzo dużych.

Znów mamy problem z mianowaniem i skalą - i znów możemy mu zaradzić poprzez zrelatywizowanie powyższego odchylenia. To znaczy, że wprowadzamy tzw. pozycyjne odchylenie ćwiartkowe:

Jest to iloraz odchylenia ćwiartkowego i mediany. Można wyrazić go w procentach. Interpretacja jest taka jak przy odchyleniu standardowym - powyżej 80 proc. cecha jest ekstremalnie zróżnicowana w zbiorowości (ale pamiętajmy, że tą zbiorowością są tu wyniki tylko z drugiej i trzeciej ćwiartki po uszeregowaniu danych rosnąco!).

Warto też sprawdzić, w którą stronę populacja bardziej odchyla się od średniej. Innymi słowy, chodzi nam o kwestię asymetrii. Podstawowy jej wskaźnik to różnica pomiędzy średnią arytmetyczną i dominantą:

W przypadku wcześniej badanych, przykładowych populacji, wynik w obu przypadkach będzie taki sam: 11,25 - 7 = 4,25. Wskazuje to na możliwość wystąpienia asymetrii prawostronnej. W istocie tak jest, bo w obu populacjach średnia arytmetyczna jest większa od mediany, ta zaś od dominanty (nie będziemy tu dowodzić zależności pomiędzy tą nierównością a asymetrią).

Można też ten sam wniosek wyprowadzić dzięki dodatkowemu narzędziu. Otóż obliczmy współczynnik skośności (asymetrii) Pearsona według poniższej formuły:

W pierwszej populacji to 0,62, w drugiej mamy 0,57. W obu przypadkach wartości za umiarkowanie wysokie, ale na pewno świadczące o asymetrii rozkładu. Jest ona prawostronna (bo wskaźnik przyjmuje wartość dodatnią, tj. średnia arytmetyczna przewyższa dominantę), co oznacza, że większość danych skupia się poniżej średniej. Jest to zapewne zgodne z nasza intuicją, biorąc pod uwagę, że w pierwszej populacji na 32 elementy aż 22 są mniejsze niż 11,25 - zaś w drugiej przy tej samej liczebności takich elementów jest 21.

Adam Witczak

BIBLIOGRAFIA:

"Wspomaganie procesów decyzyjnych. Tom I. Statystyka", red. M. Lipiec-Zajchowska, Wyd. C.H. Beck 2003.

"Metody statystyczne w zarządzaniu", red. D. Witkowska, Wydział Zarządzania i Organizacji Politechniki Łódzkiej 1999.