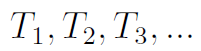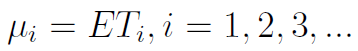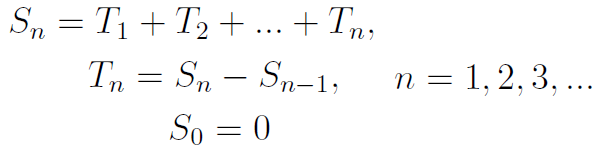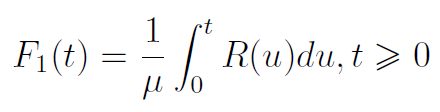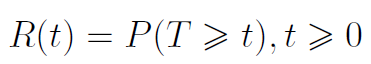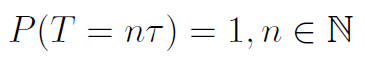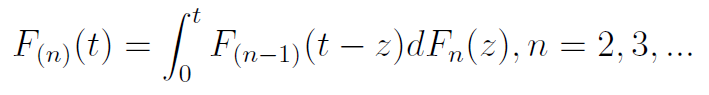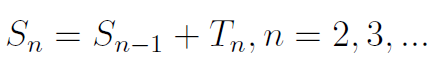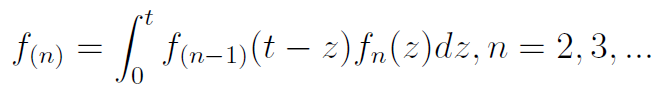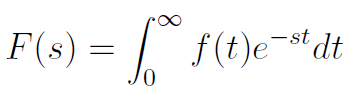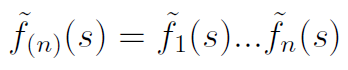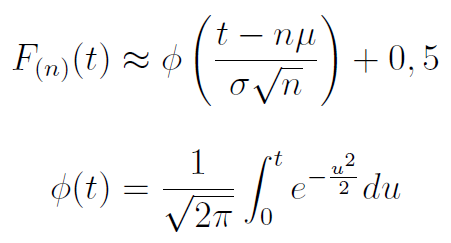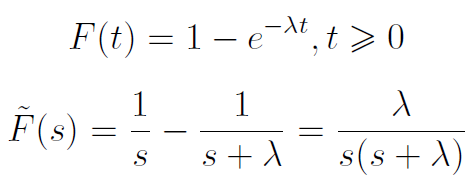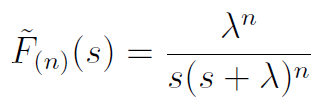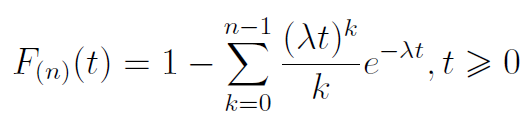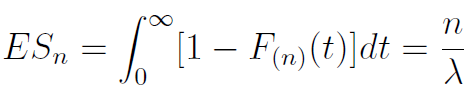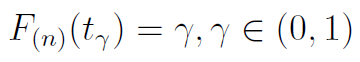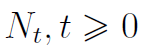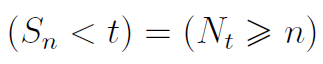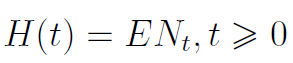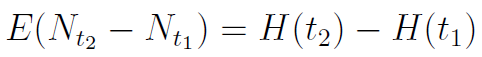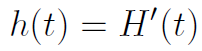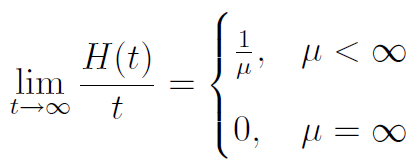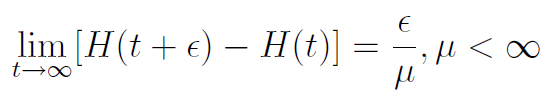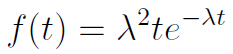Procesy odnowy w inżynierii produkcji

Teoria odnowy to jedna z gałęzi rozbudowanej dziedziny matematyki, jaką jest rachunek prawdopodobieństwa. Teoria ta ma rozmaite zastosowania ekonomiczne.

Przede wszystkim jest użyteczna w inżynierii produkcji, ponieważ przy jej pomocy modeluje się zagadnienia związane z naprawą urządzeń czy ogólnie wszelkich obiektów technicznych. Na przykład dzięki funkcji odnowy można poznać wartość oczekiwaną liczby napraw w określonym przedziale czasowym. To z kolei pozwala ocenić, ile powinno się zawczasu przygotować części zamiennych, ilu pracowników skierować na odcinek napraw, jakie będą koszty finansowe tego wszystkiego etc.

Procesy odnowy znajdują zastosowanie także w matematyce aktuarialnej, czyli związanej z ubezpieczeniami. Wówczas przez odnowy rozumie się (trochę paradoksalnie) szkody czy też wnioski o odszkodowanie. Paradoks jest zresztą pozorny, jeśli tylko przyjmiemy (dla uproszczenia), że odnowa następuje właściwie zaraz po uszkodzeniu, niejako w tym samym momencie. Można jednak rozważać także (czego w tym tekście nie robimy) tzw. alternatywne strumienie odnowy, w których uwzględnia się czas niezdatności obiektu, tj. czas wykonywania naprawy.

W Polsce teorią odnowy (i szerzej - teorią niezawodności) zajmowali się m.in. tacy uczeni jak Dobiesław Bobrowski (autor kilku książek na ten temat) czy Bolesław i Ilona Kopocińscy - małżeństwo matematyków związanych z Uniwersytetem Wrocławskim. W tym omówieniu korzystamy przede wszystkim z pracy D. Bobrowskiego (por. bibliografia).

Poniżej przedstawimy kilka pojęć podstawowych pojęć z teorii odnowy - i kilkanaście niezbędnych wzorów.

Zacznijmy od ciągu zmiennych losowych:

Można je interpretować jako czasy zdatności obiektu - najpierw do pierwszego uszkodzenia (T₁), później pomiędzy kolejnymi awariami. Naturalnie interpretacja ubezpieczeniowa też jest możliwa - są to wtedy odstępy czasu pomiędzy szkodami.

Te odcinki czasu mają swoje wartości oczekiwane:

A teraz pierwsze pojęcie stricte związane z teorią odnowy. Oto strumień odnowy, czyli ciąg zmiennych losowych, opisujących czasy do n-tej awarii:

O ile zakładamy, że zmienne losowe określające czasy pomiędzy uszkodzeniami (czyli zmienne T₁, T₂, ...) są niezależne, o tyle oczywiście nie można już tego powiedzieć o zmiennych tworzących strumień. Tu bowiem zachodzi zależność widoczna w drugim wzorze na ostatniej ilustracji.

Strumieniem prostym nazywamy taki, w którym T₁ ma taki sam rozkład jak pozostałe. Innymi słowy, czasem do pierwszej awarii rządzi to samo prawo, co późniejszymi okresami. Jeśli dodatkowo wszystkie zmienne T_i mają rozkład wykładniczy (z tym samym parametrem), to mówimy o rozkładzie Poissona.

Strumień stacjonarny to taki, w którym zachodzi następująca zależność:

Ten wzór określa dystrybuantę pierwszej zmiennej losowej, tj. T₁. Z kolei R(t) to funkcja niezawodności:

Jest to po prostu prawdopodobieństwo tego, że przynajmniej przez czas t nie dojdzie do awarii (czy zgłoszenia szkody).

Strumień może być też okresowy - gdy czasy między uszkodzeniami określone są przez dyskretne zmienne losowe oraz zachodzi zależność (dla pewnej liczby τ > 0):

Możemy rozważać dystrybuanty czasów do n-tego uszkodzenia. Każda spełnia warunek (prawa strona to tzw. splot dystrybuant):

Wynika to z faktu, że:

Owo wynikanie to po prostu zastosowanie standardowego wzoru na dystrybuantę sumy zmiennych losowych, prezentowanego na kursie rachunku prawdopodobieństwa.

Analogicznie prezentują się gęstości wspomnianych czasów:

W tym momencie przypomnijmy, czym jest transformata Laplace'a funkcji:

Otóż możemy skorzystać przy naszych gęstościach czasów ze wzoru na transformatę splotu funkcji, który daje nam iloczyn transformat:

Okazuje się, że rozkład zmiennej losowej S_n dla dużych n można przybliżać rozkładem normalnym:

Po co to wszystko? Czas na mały przykład. Wyobraźmy sobie, że czas zdatności żarówki w pomieszczeniu ma rozkład wykładniczy. Strumień odnowy jest wtedy strumieniem Poissona i dla każdej ze zmiennych losowych T₁, T₂, ... zachodzą wzory (prezentujemy i dystrybuantę, i jej transformatę):

Z kolei transformata Laplace'a dystrybuanty czasu do n-tego uszkodzenia to (z odpowiedniego wzrostu łączącego transformaty gęstości i dystrybuanty):

Z tego można otrzymać tzw. transformatę odwrotną:

Do czego jest nam ona potrzebna? Otóż można dzięki niej wyliczyć oczekiwany czas do n-tego uszkodzenia (pomijamy obliczenia, które są po drodze):

Do tego dodajmy jeszcze wzór na kwantyl t_γ rozkładu czasu do n-tego uszkodzenia:

Otóż praktyczny przykład jest taki: mamy jedną świecącą żarówkę i drugą, zapasową (na wymianę w razie awarii). Ile możemy w ten sposób zagwarantować sobie czasu oświetlania z ryzykiem wynoszącym 0,05 = 5 proc., że zapas będzie za mały? Otóż w powyższych wzorach bierzemy γ = 0,95 oraz n = 2. Przyjmijmy też, że parametr rozkładu Poissoina to λ = 0,001.

Pominiemy szczegóły obliczeń - przy wyliczaniu t_γ trzeba użyć metod numerycznych, przybliżonych. W każdym razie efekt jest taki: t_0,95 to ok. 4750, zaś t_0,05 to ok. 350. Wielkości te można interpretować jako godziny. A więc: z prawdopodobieństwem równym 95 proc. mamy co najmniej 350 godzin oświetlania (przy zadanym rozkładzie), zaś z prawdopodobieństwem 5 proc. (czyli raz na 20 przypadków) te dwie żarówki wystarczą na 4750 godzin.

Znamy już pojęcie strumienia odnowy. Blisko związany jest z nim inny termin, tj. proces odnowy:

Jest to punktowy proces losowy, o wartościach, które oznaczają liczbę odnów do chwili t. A więc np. N₅ to liczba odnów do końca piątej godziny, jeśli w takich jednostkach mierzymy czas. Przypomnijmy przy tym, że proces losowy (stochastyczny) to po prostu rodzina zmiennych losowych, indeksowana parametrem t, przebiegającym zbiór T - ale przy założeniu, że T jest podzbiorem prostej rzeczywistej, zaś t interpretowany jest jako czas. W pewnym sensie jest to jedna, ale wielowymiarowa zmienna losowa - jeśli mamy na myśli fakt, że ów ciąg zmiennych interpretujemy poniekąd jako tę samą wielkość (np. cenę akcji czy poziom opadów), tyle że w różnych momentach czasu. W każdej z tych chwil postrzegamy ową zmieniającą się wielkość jako odrębną zmienną losową.

Związek między procesem odnowy i strumieniem odnowy jest taki (równość zdarzeń):

Mamy jeszcze pojęcie funkcji odnowy, wspomniane na początku. To z kolei wartość oczekiwana procesu odnowy:

Dzięki znajomości tej funkcji możemy m.in. obliczyć oczekiwaną (średnią) liczbę uszkodzeń w danym przedziale czasu:

Rozważa się też gęstość odnowy, czyli pochodną funkcji odnowy:

Istnieją pewne twierdzenia, które obrazują zachowanie się funkcji odnowy w miarę upływu czasu. Otóż funkcja dla nieokresowego ogólnego strumienia odnowy spełnia następujący warunek asymptotyczny (tzw. elementarne twierdzenie odnowy):

Mamy też (dla strumienia nieokresowego, prostego i dla ε > 0) twierdzenie Blackwella:

Gdy mi jest nieskończone, to powyższa granica wynosi 0. Przez μ, jak na początku, rozumiemy wartość oczekiwaną zmiennej T_i, tj. ET_i. W praktyce jednak, jeśli wszystkie te zmienne mają ten sam rozkład, to będzie to średnia dla tego rozkładu.

Jakie znaczenie ma twierdzenie Blackwella? D. Bobrowski podaje następujący przykład: mamy pewne urządzenie (wirówkę) i element w niej (filtr). Jego czas zdatności jest określony tzw. rozkładem Erlanga. Jego gęstość wyraża wzór:

Gęstość, przypomnijmy, ma tę cechę, że całka oznaczona z niej (od a do b) jest równa prawdopodobieństwu, że zmienna losowa przyjmuje wartość z zakresu [a, b]. Rozkład powyższy, jak widać, ma parametry α i  λ, tu przyjmujemy α = 2 i  λ = 0,03. Otóż w rozkładzie Erlanga wartość średnia μ =2/λ.

Weźmy więc przedział długości 400 godzin (400 h). Z twierdzenia Blackwella możemy oszacować, że ε / μ = 400 * 0,015. To oznacza, że stopniowo, w miarę upływu czasu, będziemy zbliżać się do sytuacji, w której na każde 400 godzin działania wirówki filtr będzie trzeba wymieniać średnio 6 razy. Dla 200 h wynik to 3 wymiany.

Dalsze zagadnienia, których nie będziemy tu opisywać, to np. obliczanie wariancji i odchylenia standardowego liczby odnów czy badanie rozkładu czasu do następnego uszkodzenia. Rozważa się też, jak pisaliśmy na początku, scenariusz, w którym czasy użytkowania przeplatają się z czasami niezdatności urządzenia. Jeszcze innym tematem są odnowy profilaktyczne, czyli odnowy - na wszelki wypadek - obiektów, które jeszcze są zdatne do użytku. Pojawia się więc problem tego, w jaki sposób takie działania rozmieścić w czasie, a więc jak zbudować odpowiednią (ekonomicznie opłacalną) strategię odnów profilaktycznych.

Adam Witczak

BIBLIOGRAFIA:

D. Bobrowski, "Modele i metody matematyczne teorii niezawodności", WNT 1985

A. D. Wentzell, "Wykłady z teorii procesów stochastycznych", PWN 1980

R. Rudnicki, "Wykłady z analizy matematycznej", PWN 2006