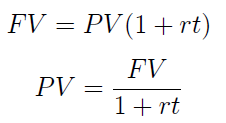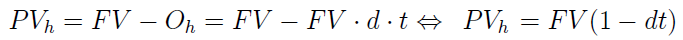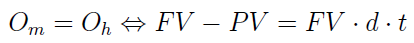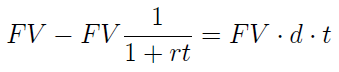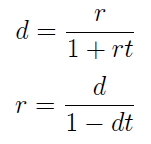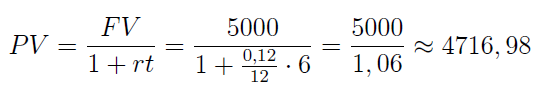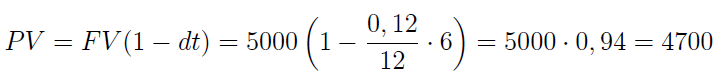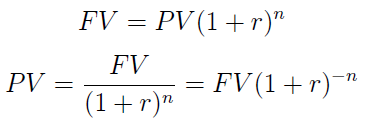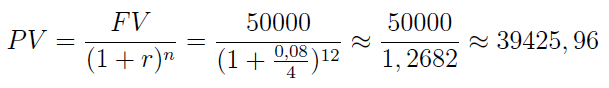Dyskontowanie na trzy sposoby

Pojęcie dyskonta (czy też dyskontowania) ma w matematyce finansowej przynajmniej trzy znaczenia. Dwa pierwsze dotyczą procentu prostego, trzecie natomiast złożonego. Najpierw zajmiemy się kapitalizacją prostą.

Otóż z jednej strony możemy tu mówić o dyskoncie matematycznym (tzw. rzeczywistym), z drugiej zaś - o dyskoncie handlowym. 

Pierwsza interpretacja wiąże się np. z obliczaniem kwoty pieniędzy, którą trzeba złożyć teraz w banku, aby w przyszłości - przy ustalonej stopie procentowej - odebrać pożądaną sumę oczekiwaną, przyszłą (FV - future value). Inny przykład to kredyt lombardowy.

Druga interpretacja dotyczy ceny zakupu certyfikatu depozytowego oraz dyskontowania weksli. To właśnie jest dyskonto handlowe.

Spójrzmy na wzór, przy pomocy którego określa się PV w pierwszym rozumieniu:

Rzecz jest prosta - i wynika z szybkiego przekształcenia standardowego wzoru na wartość przyszłą przy oprocentowaniu prostym.

W drugim ujęciu rozważamy wielkość oznaczoną jako PV_h, by odróżnić tak pojętą wartość obecną od tej, która pojawiła się wcześniej.

W tym wzorze pojawia się odrębna stopa - mianowicie stopa dyskontowa d. Odsetki oblicza się zatem od wartości końcowej FV. Te właśnie odsetki określa się mianem dyskonta. A zatem jeśli dłużnik ma zwrócić po upływie określonego czasu kwotę FV, to w momencie bieżącym otrzymuje ją pomniejszoną o kwotę O_h (moglibyśmy tu użyć także symbolu D, to oczywiście tylko kwestia przyjętych oznaczeń).

Stopa dyskontowa jest czymś innym niż procentowa - nie są one równoważne (nawet jeśli nominalnie mają tę samą wartość; zobaczymy to jeszcze na przykładach). Można jednak sprawdzić, jaka relacja je wiąże. Innymi słowy, przekonamy się, jaka musi być stopa procentowa, by odsetki z jej tytułu były takie jak dyskonto handlowe, tj. jak odsetki generowane przy pomocy ustalonej stopy dyskontowej.

Załóżmy zatem, że odsetki w obu ujęciach są równe. Wówczas możemy napisać:

Po prawej stronie znaku logicznej równoważności mamy równość, której lewa część to rozpisanie odsetek rzeczywistych, a prawa - tych liczonych według metody dyskontowania handlowego. Rozpiszmy jeszcze lewą stronę równości:

Stąd łatwo możemy otrzymać następujące zależności:

To właśnie wynik, który zapowiadaliśmy. Wypada sprawdzić rzecz na przykładach. Załóżmy, że ktoś zaciąga kredyt lombardowy. Wie, że po sześciu miesiącach ma spłacić 5000 zł, przy czym stopa procentowa to 12 proc. Jaką kwotę otrzymuje od banku obecnie?

Przypomnijmy, stosujemy tu metodologię dyskonta matematycznego:

Na wszelki wypadek wyjaśnijmy, co dzieje się w mianowniku. Otóż jeśli mówimy o stopie 12 proc., to jest to stopa roczna - tak się domyślnie przyjmuje - a nie stopa za 6 miesięcy. Tę musimy obliczyć - poprzez obliczenie stopy za 1 miesiąc (stąd dzielenie 0,12 / 12) i przemnożenie jej sześciokrotnie. Oczywiście równie dobrze moglibyśmy po prostu podzielić 0,12 przez 2 (bo  rok zawiera dwa sześciomiesięczne półrocza). Ostatecznie okazuje się, że klient otrzymuje do ręki prawie 4717 zł.

Weźmy teraz analogiczne dane, ale dla dyskonta handlowego. Nominał weksla to 5000 zł, termin wykupu to 6 miesięcy, stopa (teraz już dyskontowa!) to 12 proc. Klient zaciąga w ten sposób kredyt dyskontowy - tzn. otrzymuje dziś pewną kwotę pieniędzy i za pół roku ma zwrócić 5000 zł. Ile dostaje teraz?

Tym razem wynik jest elegancki: równo 4700 zł. Jest to jednak suma wyraźnie niższa niż ta, którą obliczyliśmy pierwszą metodą. Ogólnie jest tak, że kapitał początkowy otrzymany po dyskontowaniu rzeczywistym wartości FV jest większy niż ten, który dostajemy po dyskontowaniu handlowym. Dyskontowanie matematyczne jest przy tym po prostu odwrotnością zwykłego oprocentowania prostego, czego nie można powiedzieć o dyskontowaniu handlowym.

Przejdźmy jeszcze do trzeciej koncepcji, tj. do dyskontowania przy procencie składanym. Jest to w zasadzie adaptacja dyskontowania rzeczywistego (matematycznego), ale w systemie kapitalizacji złożonej. Spójrzmy na wzory:

W pierwszej linijce mamy obliczenie wartości przyszłej, w drugiej - wartości obecnej, teraźniejszej. Tę właśnie procedurę określamy mianem dyskontowania złożonego. Czynnik (1+r)^-n nazywamy współczynnikiem dyskontującym lub też mnożnikiem wartości obecnej.

Oto standardowy przykład: ile należy wpłacić do banku, by po 3 latach odebrać 50 tys. zł? Załóżmy przy tym, że kapitalizacja jest kwartalna, zaś oprocentowanie to 6 proc. (oczywiście - rocznie).

Wykonajmy obliczenia:

Tym razem 8 proc. (tj. 0,08) dzielimy na 4, by otrzymać stopę kwartalną (naturalnie moglibyśmy też wykonać dzielenie przez 12, a otrzymany wynik przemnożyć przez 3, bo tyle miesięcy ma kwartał). Potęgujemy do 12, bo tyle jest kwartałów w ciągu 3 lat. Ostatecznie okazuje się, że do banku należy wpłacić ok. 39,42 tys. zł. Pomijamy tu prowizję banku czy ew. inne koszty.

Adam Witczak

BIBLIOGRAFIA:

M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN 2005

B. Nalepa, Matematyka finansowa - materiały pomocnicze dla studentów, WSBiF Katowice 1997