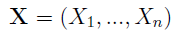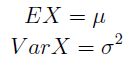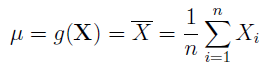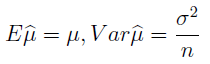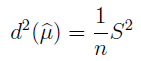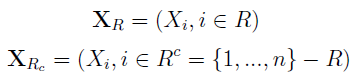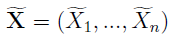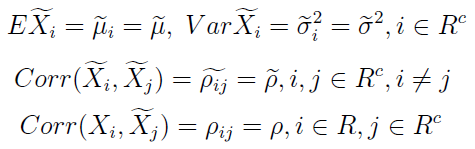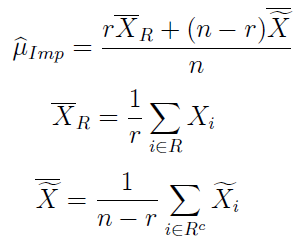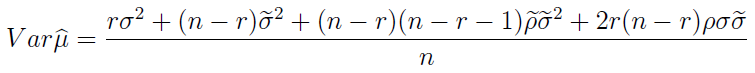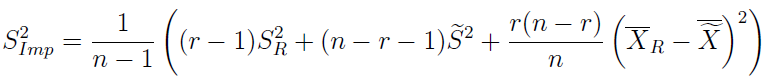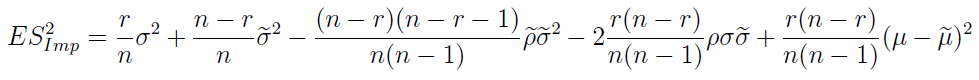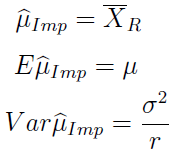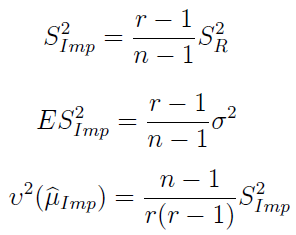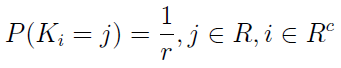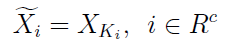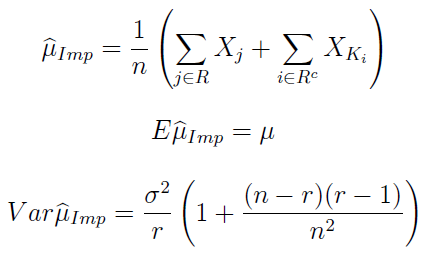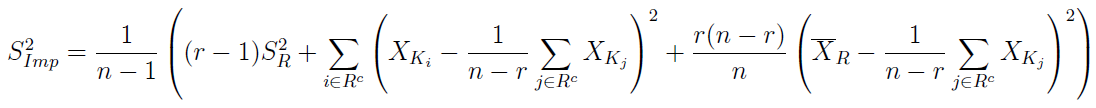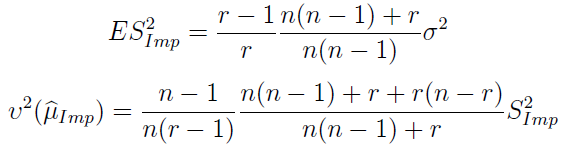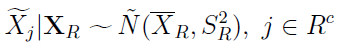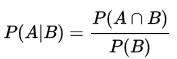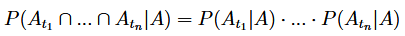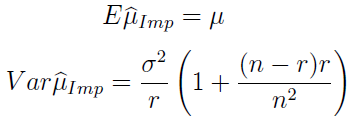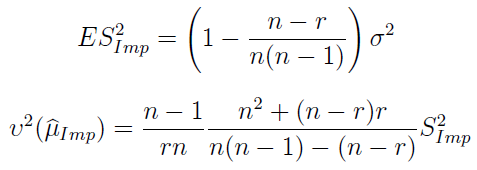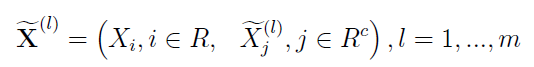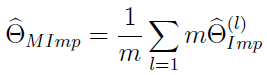Techniki imputacji w statystyce

W rozmaitych zastosowaniach statystyki zdarza się, że w badanej próbce brakuje niektórych danych. Różne tego typu sytuacje można sobie wyobrazić w kontekście badań chemicznych, fizycznych, socjologicznych czy wreszcie - ekonomicznych (finansowych).

Na przykład niektóre dane mogły zwyczajnie zaginąć w wyniku awarii komputera czy przypadkowego usunięcia plików (albo archiwów papierowych). Mogło zdarzyć się tak, że ankieterzy nie dotarli do wszystkich respondentów - lub też, że respondenci nie chcieli udzielić odpowiedzi. D. Grochowina podaje następujący przykład: prognozowanie upadłości przedsiębiorstw obnaża problem braku danych, który dotyczy głównie podmiotów z problemami finansowymi, pragnących w ten sposób zataić złą kondycję.

Bywa i tak, że mamy mocne powody, by niektóre odczyty uważać za niewiarygodne. Respondent może przedstawiać fakty w sposób nadmiernie dla siebie korzystny. To także kwestia niedoskonałości aparatury pomiarowej, jeśli z takiej korzystamy: czasami urządzenie nie wychwyci pewnych zjawisk albo przedstawi je w sposób zniekształcony czy niejednoznaczny.

Zostajemy więc z wektorem danych, w którym pewne miejsca są puste, a przynajmniej tak musimy je traktować. Jeżeli tych luk nie jest zbyt wiele, a zarazem mamy dobry powód, by sądzić, że brakujące dane są (czy też - byłyby) w miarę zbliżone do posiadanych, to możemy spróbować uzupełnić nasze odczyty. Oczywiście wypada to zrobić w sposób możliwie uczciwy i sensowny. Najbardziej obiektywnym tego kryterium będzie oczywiście matematyka.

Techniki imputacji to zaawansowane (to słowo zawsze budzi respekt, czyż nie?) metody statystyki matematycznej, służące uzupełnianiu próbek. W poniższym opracowaniu omówimy zupełne podstawy tego zagadnienia. Bazować będziemy przede wszystkim na pracy J. Wesołowskiego i J. Tarczyńskiego (por. bibliografia), referując zasadnicze punkty jej pierwszych rozdziałów - ale skorzystamy także z innych źródeł.

I tu wypada poczynić pewną uwagę. Otóż czytelnik nastawiony matematycznie, dobrze zaznajomiony ze statystyką i modelowaniem finansowym, może nam zarzucić, że nie prezentujemy właściwie żadnych dowodów prezentowanych twierdzeń. To prawda, ale taka prezentacja nadmiernie poszerzyłaby ramy artykułu, który i tak już wykracza poza konwencję tekstu "popularnego". Dowody te zresztą są w dużym stopniu żmudnymi rachunkami, opartymi o wcześniejsze wzory i znane zależności, a pracę Wesołowskiego i Tarczyńskiego można znaleźć na stronach GUS.

Z drugiej strony, ktoś słabo zaznajomiony z matematyką może uznać, że przedstawiamy po prostu katalog dziwnych, skomplikowanych formuł. To również jest prawdą, ale czujemy się usprawiedliwieni. W rzeczywistości każdy, kto chce na poważnie zajmować się zagadnieniami finansowymi, aktuarialnymi czy ekonomicznymi, w którymś momencie zetknie się z wyższym aparatem matematycznym. Od tego nie ma ucieczki - i trzeba przeboleć fakt, że np. w statystyce wzory bywają długie i złożone. Warto przekonać się o tym zawczasu. Przejdźmy jednak do rzeczy.

Podstawy

W ogólności rozważamy pewną próbkę danych, którą możemy traktować jako wektor zmiennych losowych:

Zakładamy niezależność tychże zmiennych oraz to, że mają jednakowe rozkłady. A więc można powiedzieć, że każda zmienna X_i ma taki sam rozkład jak pewna zmienna X, której wartość oczekiwaną i wariancję oznaczamy następująco:

W normalnych warunkach (na razie nie mówimy nic o imputacji) średnią, tj. wartość oczekiwaną, estymuje się następującą funkcją:

Jest to więc estymator średniej: funkcja, która przybliża nam, na podstawie danych z próbki, średnią dla całej populacji. Innymi słowy, wnioskujemy np. o przeciętnym wzroście wszystkich Polaków na podstawie wzrostu wybranego tysiąca obywateli. Jak widać, podstawowa metoda jest banalna: liczymy po prostu średnią arytmetyczną. Co więcej, można pokazać - i jest to ogólna prawidłowość matematyczna - że estymator ten jest nieobciążony, a więc, że jego wartość oczekiwana będzie równa autentycznej średniej. Widzimy to poniżej, przy czym bonusowo mamy tu również wzór na wariancję estymatora:

Uwaga co do ostatniego zdania: nie chodzi (jeszcze) o estymator wariancji, ale o wariancję estymatora przybliżającego średnią. On przecież też może mieć swoją wariancję i odchylenie standardowe, dlaczego nie?

Estymacja wariancji z próby oczywiście też jest brana pod uwagę:

Ten estymator też jest nieobciążony, co widzimy w drugim wierszu powyższego obrazka. Jego wartością oczekiwaną jest autentyczna wariancja z populacji.

I jeszcze jedna rzecz (znów należy uważnie patrzeć na kolejność słów): nieobciążony estymator wariancji estymatora średniej:

A zatem wariancję estymatora średniej też można... estymować, przybliżać. Skomplikowane? A nawet jeszcze na dobre nie zaczęliśmy. Ale już zaczynamy.

Dane, których brakuje

Mamy n indeksów w wektorze, ale przyjmiemy teraz, że udało się nam faktycznie zaobserwować tylko odczyty z pewnego podzbioru indeksów, oznaczonego literą R:

W takim razie mamy jeszcze dopełnienie R, czyli R^c - pozostałe miejsca. To luki, o których była mowa we wprowadzeniu. Zatem wyjściowy wektor można postrzegać jako złożony z dwóch podwektorów:

Teraz zapiszmy schemat próbki, w której uzupełniliśmy dane - na razie pomijamy to, skąd wzięliśmy "bonusowe" odczyty, tj. jakiej techniki imputacji użyliśmy.

Na miejscach należących do podzbioru R nie zmieniamy nic, X_i "z falką" pozostaje taki sam jak pierwotnie, ale na miejscach z R^c wstawiamy nowe, imputowane zmienne. Jest to już więc nowa próbka, nie ma w niej luk, pustych miejsc.

Przyjmuje się następujące założenia:

Na razie nie musimy się nimi martwić. W każdym razie widać, że zakładamy m.in., iż zmienne imputowane mają jednakowe wartości oczekiwane i wariancje. Taka sama jest też korelacja między każdymi dwiema.

Imputacja - ujęcie ogólne

I dopiero teraz przechodzimy do rzeczy. Otóż jeśli dany parametr (np. średnia czy wariancja) jest estymowany przy pomocy pewnej funkcji (np. średniej arytmetycznej), to imputacyjny estymator tego parametru nie jest niczym innym jak zastosowaniem tej funkcji do nowej próbki.

A zatem imputacyjny estymator średniej wygląda tak:

Przez r rozumiemy tutaj liczebność zbioru R, tj. liczbę indeksów z prawdziwymi obserwacjami.

Można pokazać, że estymator ten jest obciążony, a jego wartość oczekiwana i obciążenie prezentują się jak poniżej:

Jeżeli wartość oczekiwana estymatora średniej dla danych prawdziwych jest taka sama jak wartość oczekiwana estymatora średniej dla danych dołączonych - to wówczas wyrażenie w nawiasie zeruje się, zatem zeruje się cały iloczyn i obciążenie znika. W takim szczególnym przypadku mamy estymator nieobciążony.

Wariancja imputacyjnego estymatora średniej wygląda tak:

Tak natomiast prezentuje się imputacyjny estymator wariancji z próbki (to co innego niż przed chwilą, powtórzmy raz jeszcze):

Dla formalności przedstawmy jeszcze jeden, cokolwiek makabryczny wzór - na wartość oczekiwaną imputacyjnego estymatora wariancji:

Można wziąć chwilę oddechu - tylko po to, by uświadomić sobie, że nic jeszcze nie powiedzieliśmy o tym, w jaki sposób możemy wprowadzić brakujące dane. To znaczy: czym zastąpić luki.

Imputacja średnią

Najprostszą metodą jest tzw. imputacja średnią. Obliczamy średnią arytmetyczną z danych zaobserwowanych - i następnie tę średnią wstawiamy w każde puste miejsc. Na przykład z wektora (2, 3, 3, 4, 5, 5, 6, _, _,) robimy wektor (2, 3, 3, 4, 5, 5, 6, 4, 4). Ale to przecież nie wszystko, bo interesuje nas nie zabawa samą próbką, ale estymowanie na jej podstawie cech całej populacji, być może wielokrotnie większej.

Poniżej widzimy imputacyjny estymator wartości oczekiwanej przy imputacji średnią, a także jego wartość oczekiwaną i wariancję:

Okazuje się, że wzory wyglądają bardzo prosto i chyba nawet nie są szczególnie zaskakujące. W szczególności oczywiste jest to, w jaki sposób dwa ostatnie wynikają z pierwszego. Wszystko można jednak wyprowadzić także z prezentowanych wcześniej formuł ogólnych, acz rachunki zajęłyby kilka linijek.

W każdym razie estymatorem imputacyjnym okazuje się po prostu zwykła średnia z tego, co byliśmy w stanie rzeczywiście zaobserwować.

Poniżej imputacyjny estymator wariancji, a zaraz po nim: jego wartość oczekiwana i nieobciążony estymator wariancji estymatora średniej.

Imputacja średnią wydaje się dość brutalna, a poza tym mało sensowna, jeśli np. rozstęp pomiędzy danymi obserwowanymi jest bardzo duży. Można sobie wyobrazić zastosowanie zamiast średniej arytmetycznej innej miary, np. mediany; ale my zajmiemy się podejściem określanym jako hot-deck.

Technika hot-deck

Technika hot-deck polega na tym, że na pustych miejscach w próbce kładziemy wartości wylosowane spośród elementów zaobserwowanych. Wyobraźmy sobie, że mamy wektor (1, 3, 3, 5, 6, 9, _, _) i dwa razy losujemy spośród sześciu widocznych liczb. Przypuśćmy, że uzyskujemy 1 i 6. Wtedy nowa próbka przybiera postać (1, 3, 3, 5, 6, 9, 1, 6). Zawsze to jakiś pomysł.

Sformalizujmy to, rozważając losowanie proste ze zwracaniem. Przez K_i rozumieć będziemy numer elementu wylosowany dla i-tej luki (w powyższym przykładzie K₂ to 6). Zmienne losowe K_i, gdzie i należy o R^c, są niezależne i mają ten sam rozkład:

Niezależne są również wektory losowe złożone odpowiednio z nowych i starych danych:

Tworząc nową próbkę, na brakujących miejscach podstawiamy zatem to, co wylosowaliśmy:

Zastosowanie ogólnych formuł, prezentowanych wcześniej, prowadzi do następującego wzoru na imputacyjny estymator wartości oczekiwanej:

Tradycyjnie już przedstawiamy go wraz z jego wartością oczekiwaną (jak widać, jest taka sama, jak dla danych obserwowanych) i wariancją (tu rzecz się trochę komplikuje).

I znów powtarzamy cykl: czas na imputacyjny estymator wariancji z próbki:

Dalej ponownie mamy wartość oczekiwaną tegoż estymatora oraz nieobciążony imputacyjny estymator wariancji imputacyjnego estymatora średniej:

Okazuje się, że dla dużych wartości r wartość oczekiwana estymatora wariancji zbiega do wariancji z zaobserwowanej części próby. Czyli S²_Imp jest w przybliżeniu nieobciążony.

***

Losowanie proste jest... proste. I ma swoje wady. Stąd też rozważa się sytuację, w której próbka pochodzi z rozkładu normalnego N(μ, σ²). Zmienne imputowane generuje się w sposób niezależny z rozkładu, w którym w miejscu μ i σ są wartości wyliczone z próby:

Można więc powiedzieć, że te zmienne imputowane są warunkowo niezależne pod warunkiem X_R. Wypada tu przypomnieć, że prawdopodobieństwo warunkowe liczymy takim wzorem:

Warunkowa niezależność zdarzeń pod warunkiem A oznacza zaś następującą równość:

Powtarzamy teraz nasz cykl. Wartość oczekiwana imputacyjnego estymatora średniej oraz jego wariancja wyglądają obecnie tak:

Z kolei estymator wariancji i nieobciążony estymator wariancji estymatora średniej mamy tu:

Powyższe wzory można wyprowadzić z ogólnych zależności z pierwszego rozdziału. Nie potrzeba do tego nawet znać jawnej postaci estymatora średniej.

Imputacja wielokrotna

Pominiemy w naszych rozważaniach wiele kwestii, np. imputację regresyjną. Wspomnimy jednak - zresztą bardzo pobieżnie - o imputacji wielokrotnej. Podejście to wprowadził i opisał Rubin w roku 1987. Idea jest poniekąd naturalna: generujemy (być może tą samą metodą) kilka próbek imputacyjnych (albo więcej, zależnie od tego, jaką chcemy osiągnąć dokładność i jakie są moce obliczeniowe naszego komputera). Następnie budujemy estymator uśredniający uzyskane wersje.

A zatem mamy taki wektor:

Zapis może być trochę mylący, ale chodzi po prostu o to, że mamy dwie serie danych: obserwowane i dodane. Te ostatnie są jednak dodawane w l powtórzeniach, za każdym razem są trochę inne. Dostajemy więc rodzinę nowych próbek, indeksowaną wskaźnikiem l od 1 do m.

Przypuśćmy, że interesuje nas jakiś parametr θ, nie precyzujemy jaki (może wartość oczekiwana, może wariancja). Otóż wtedy estymator wielokrotnej imputacji Rubina wygląda tak:

Jest to więc po prostu średnia arytmetyczna z estymatorów imputacyjnych (wyliczonych osobno) dla wszystkich próbek.

Ale dalej zaczynają się schody, na które nie będziemy już wchodzić. Ostatecznie miał być to przecież tylko luźny wstęp. Czytelnik może się żachnąć, bo przecież w odpowiednich programach (jak R czy Statistica) nierzadko wystarczy wpisać odpowiednią procedurę albo wręcz kliknąć przycisk - i komputer wyliczy to, co chcemy. To prawda, ale warto zawsze wiedzieć, co dzieje się w środku - jakie formuły są stosowane, czym się różnią, jakie mają własności matematyczne. Być może "sucha teoria" to tylko martwy szkielet - ale nie ma prawdziwych zastosowań bez znajomości i zrozumienia podstaw teoretycznych.

Adam Witczak


BIBLIOGRAFIA:

J. Wesołowski, J. Tarczyński, Podstawy matematyczne technik imputacyjnych, Wiadomości Statystyczne nr 9/2016 (664).

Janusz L. Wywiał, Wprowadzenie do wnioskowania statystycznego, Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2012.

D. Grochowina, Wpływ metod imputacji danych na skuteczność klasyfikacyjną modelu logitowego zastosowanego do prognozowania upadłości przedsiębiorstw, Acta Universitatis Nicolai Copernici, Vol. 45, no. 2 (2014).

D. B. Rubin, An Overview of Multiple Imputation, Proceedings of the Survey Research Methods Section, American Statistical Association 1988.

Ł. Dębowski, Własności entropii nadwyżkowej dla procesów stochastycznych nad różnymi alfabetami, rozprawa doktorska IPI PAN.

J. Jóźwiak, J. Podgórski, Statystyka od podstaw, Polskie Wydawnictwo Ekonomiczne 1998.