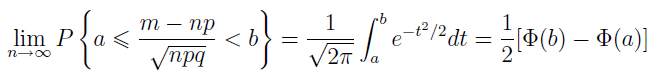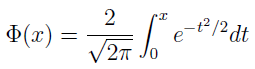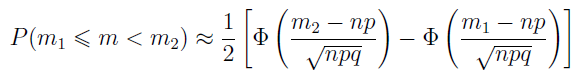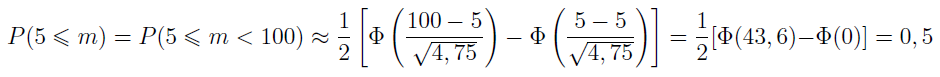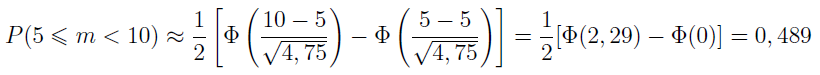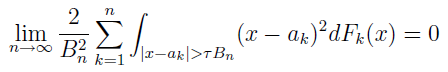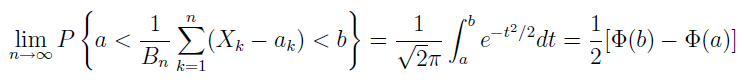Twierdzenie de Moivre'a-Laplace'a

Twierdzenie de Moivre'a-Laplace'a zaliczane jest do tzw. twierdzeń granicznych rachunku prawdopodobieństwa. A zatem opisuje nam ono rozkład sumy niezależnych zmiennych losowych, których liczba zmierza do nieskończoności. Inaczej rzecz ujmując, przybliża nam zachowanie się tejże sumy.

Przejdźmy do rzeczy. Twierdzenie de Moivre'a-Laplace'a odnosi się do sytuacji, w której wykonujemy n niezależnych doświadczeń losowych. Na przykład sprawdzamy wyroby wyprodukowane w fabryce (pod kątem ich sprawności). W każdym doświadczeniu z tym samym prawdopodobieństwem może wystąpić zdarzenie A, np. uszkodzenie (wadliwość) wyrobu. Wówczas zachodzi następująca równość:

Wzór zdaje się być dość skomplikowany i pewnie taki jest, ale w rachunku prawdopodobieństwa i statystyce nigdy od tego całkowicie nie uciekniemy. W każdym razie byłoby to trudne na etapie szkoły wyższej. Trzeba się z tym pogodzić, a czytelnikom źle trawiącym rozbudowane formuły matematyczne możemy tylko powiedzieć na pocieszenie, iż pomijamy dowód twierdzenia.

Oznaczenia są takie: m to ilość wystąpień zdarzenia A, n to liczba doświadczeń, zaś:

to tzw. funkcja Laplace'a. Jest ona wyrażona przy pomocy całki. Nie musimy jej obliczać ręcznie: jej wartości, przynajmniej te, których się zwykle używa, są ujęte w tablicach, które można znaleźć w książkach z obszaru statystyki i probabilistyki (por. bibliografia).

Pokażemy na przykładzie, jak ten mechanizm działa. Odwołajmy się do podanego wcześniej obrazu fabryki i sprawdzania jakości produktów. Załóżmy, że wiemy skądinąd, iż prawdopodobieństwo zepsucia się urządzenia w czasie sprawdzania jego niezawodności wynosi p = 0,05 (tj. 5 proc.). Zapytajmy teraz, jakie jest prawdopodobieństwo tego, że przy testowaniu 100 urządzeń zepsuje się ich mniej niż 5?

Twierdzenie Moivre'a-Laplace'a mówi nam, że jeśli zdarzenie zachodzi nie więcej niż m₂ razy, ale nie mniej niż m₁ razy, to zachodzi zależność:

Oczywiście q = 1 - p. A zatem u nas m₁ = 5, m₂ = 100, n = 100, p = 0,05, q = 0,95. Stąd:

Tak więc szansa, iż w 100 wyrobach co najmniej 5 zostanie uszkodzonych, to 50 proc.

A jeśli interesuje nas sytuacja, w której takich przypadków będzie więcej niż 5, wszelako mniej niż 100? Voila:

Tym razem wartość jest nieco niższa, mamy blisko 49 proc.

Podamy jeszcze twierdzenie Lapunowa, bardziej skomplikowane - przynajmniej w zapisie. Załóżmy mianowicie, że mamy ciąg zmiennych losowych X₁, X₂, ..., X_n. Niech ciąg ten dla każdego τ > 0 spełnia tzw. warunek Lindeberga:

Wtenczas twierdzenie Lapunowa mówi, iż zachodzi następująca równość graniczna:

Oznaczenia są takie: F_k(x) to dystrybuanta zmiennej losowej X_k, a_k = E(X_k) to wartość oczekiwana zmiennej X_k, b_k²= D²(X_k) to wariancja zmiennej X_k, zaś B_n² to suma wyrazów b_k² liczona od 1 do n.


Adam Witczak

BIBLIOGRAFIA:

"Problemy rachunku prawdopodobieństwa", praca zbiorowa, PWN 1966.

J. Jakubowski, R. Sztencel, "Rachunek prawdopodobieństwa dla (prawie) każdego", SCRIPT 2006.

R. Magiera, "Modele i metody statystyki matematycznej", Oficyna Wydawnicza GiS 2005