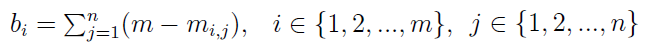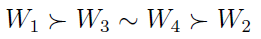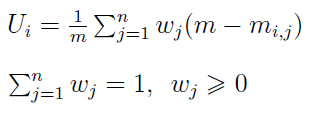Metoda Bordy w analizie wielokryterialnej

Metoda Bordy to dość prosta technika wielokryterialnego wspomagania decyzji. W swej podstawowej formie nie wymaga nawet znajomości matematyki wyższej: nie wykorzystuje żadnych skomplikowanych narzędzi analizy, algebry czy logiki.

Oczywiście metoda Bordy ma liczne warianty - i niektóre z nich są oczywiście bardziej skomplikowane, na przykład wykorzystują teorię zbiorów rozmytych. Podstawowy model jest jednak łatwy do opisania. Dodajmy jeszcze, nim przejdziemy do rdzenia naszego wywodu, że metdoa została nazwana na cześć Jana Karola Bordy, francuskiego fizyka i matematyka, żyjącego w latach 1733 - 1799.

Załóżmy, że mamy m wariantów i n kryteriów. Na przykład chcemy wybrać najlepszą spośród m nieruchomości, biorąc pod uwagę kryteria takie jak cena, powierzchnia czy stan techniczny. Można też wyobrazić sobie wybór przedsięwzięcia, w które mielibyśmy zainwestować nasz kapitał.

Otóż clou metody jest takie: za najlepsze uważamy te warianty, które mają najwyższą tzw. liczbę Bordy. Ta natomiast wyraża się poniższym wzorem:

Obliczamy, jak widać, liczbę dla i-tej spółki, czyli b_i - i-tą liczbę Bordy. Sumujemy wyrażenia, w których od m (czyli liczby scenariuszy) odejmuje się miejsce, które dany wariant zajmuje w świetle j-tego kryterium. Lokaty te uszeregowane są od najlepszych (najkorzystniejszych) do najgorszych.

Innymi słowy, wyrażenie w nawiasie pokazuje nam, jak daleko dany wariant jest od pierwszego miejsca w odniesieniu do określonego kryterum. Te właśnie "odległości" sumujemy.

*

Zobaczmy, jak to działa. Przykład niech będzie taki: mamy m = 4 nieruchomości. Są to magazyny. Chcemy zakupić "najlepszy" z nich. Co nas interesuje? Załóżmy, że rozważamy 6 kryteriów:

- K₁ - powierzchnia w metrach kwadratowych; zasadniczo chcemy kupić jak największy magazyn

- K₂ - cena za metr kwadratowy; interesuje nas, by była jak najniższa

- K₃ - cena za cały budynek; tu również najniższa jest tą najlepszą

- K₄ - odległość w kilometrach od siedziby naszej firmy; chcemy ją zminimalizować - magazyn powinien być możliwie blisko

- K₅ - wyposażenie budynku; przyjmujemy, że jesteśmy w stanie ocenić je w skali od 0 (brak wyposażenia, stan surowy, scenariusz najgorszy) do 3 (budynek jest gotów do natychmiastowego użytku: zawiera regały, wózki i w ogóle wszystko, czego potrzebujemy). A zatem w tym wypadku wyższe wartości są lepsze.

- K₆ - wiek budynki; chcemy, by magazyn był jak najmłodszy.

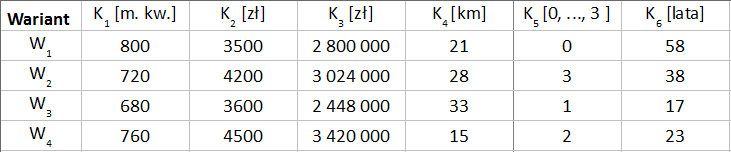
Spójrzmy na tabelkę:

Widzimy np., że scenariusz W₁ daje nam największą powierzchnię i najniższą cenę za metr kwadratowy, ale np. jego wyposażenie prezentuje się najgorzej. Propozycja W₂ jest gotowa do użytku, ma wszystkie niezbędne urządzenia. Z kolei wariant W₃ to budynek najmłodszy (ma tylko 17 lat), ale i najbardziej od nas oddalony (aż o 33 km), a do tego najmniejszy. Wariant W₄ jest najbliżej (15 km), ale jest najdroższy (tak w przeliczeniu na metr, jak i w ogóle).

Ale z takich dywagacji niewiele nam przyjdzie: trudno określić, który wariant jest "najlepszy". Każdy ma wady i zalety. Metoda Bordy daje pewien sposób, w jakiejś mierze arbitralny, ale jednak pomocny.

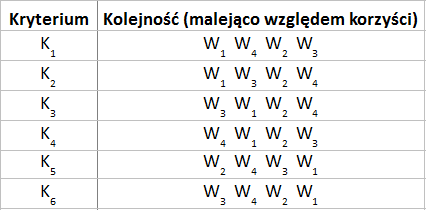
Zerknijmy na drugą tabelkę. Warianty zostały w niej uszeregowane od najlepszych do najgorszych w świetle poszczególnych kryteriów.

Pojawiają się tu wszystkie fakty i zależności opisane wcześniej, a także wiele innych. Na przykład W₂ jest lepszy od W₃ w tym sensie, że ma większą powierzchnię, ale gorszy przez to, że jest od niego dużo starszy.

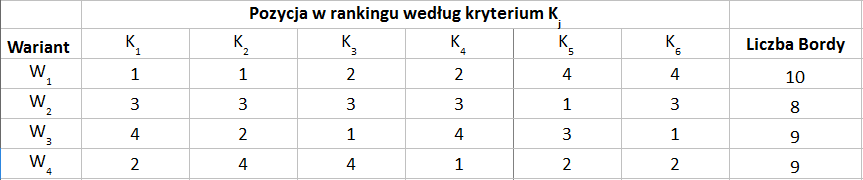
W trzeciej tabeli prezentujemy pozycje, jakie dany wariant zajmuje w rankingu (im niższa pozycja, tym lepiej: od pierwszego do czwartego miejsca).

Na przykład wariant W₂ jest pierwszy (nr 1) według kryterium K₅, zaś W₄ jest drugi z perspektywy K₁, K₅ i K₆.

W tabeli mamy już wyliczone liczby Bordy. I to już właściwie wszystko, co istotne. Okazało się, że najlepszy scenariusz to W₁ (mamy 10 pkt), W₃ i W₄ są trochę gorsze (i nieporównywalne ze sobą, oba mają po 9 pkt), zaś W₂ prezentuje się z wynikiem 8 pkt najsłabiej.

W zapisie symbolicznym podsumowanie wygląda następująco:

Model, który zaprezentowaliśmy, nie uwzględnia wag. Wszystkie kryteria są tak samo istotne. Oczywiście w praktyce nie musi tak być. Przeciwnie, ktoś mógłby powiedzieć, że niska cena za metr kwadratowy jest dla niego ważniejsza niż wyposażenie budynku.

W takiej sytuacji modyfikujemy liczbę Bordy, stosując zasadę tzw. SAR - ważonego wskaźnika sumacyjnego (Simple Additive Ranging). Oto i nowy wzór:

Nie jest on szczególnie zaskakujący: tym razem "odległości od pierwszego miejsca" mnożymy przez odpowiednie wagi, a sumę dodatkowo dzielimy przez liczbę wariantów. Wagi to oczywiście liczby z przedziału [0, 1], które się sumują do 1. Finalna wartość SAR, tj. U_i, też zawiera się w zakresie [0, 1].


Adam Witczak


BIBLIOGRAFIA:

A. Kobryń, "Wielokryterialne wspomaganie decyzji w gospodarowaniu przestrzenią", Difin 2014.

J. Michnik, "Wielokryteriane metody wspomagania decyzji w procesie innowacji", Wyd. Uniwersytetu Ekonomicznego w Katowicach 2013.