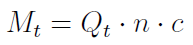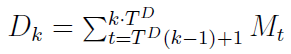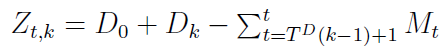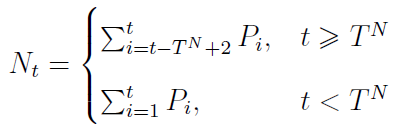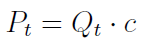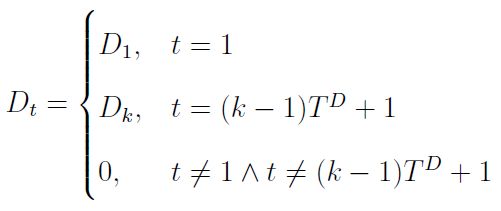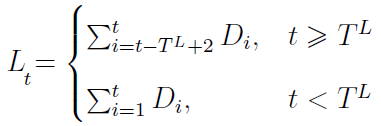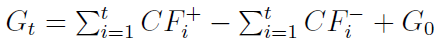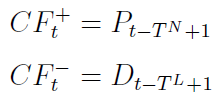Progozowanie majątku obrotowego

W każdym przedsiębiorstwie trzeba myśleć nie tylko o teraźniejszości, ale również o przyszłości. Nigdy jej nie znamy, tym niemniej możemy określać jej obraz w przybliżeniu. To przybliżenie zależeć będzie zarówno od danych historycznych, jak i od naszych planów czy zamierzeń, a wreszcie - od losowych czynników (w szczególności zewnętrznych), na które nie mamy wpływu.

Firmy dość często prezentują inwestorom i kontrahentom prognozy swego rozwoju. Zapowiadają np., że mają zamiar osiągnąć pewien poziom przychodów, zysków czy wskaźników bilansowych. Aby taką prognozę sporządzić, trzeba jednak wpierw skupić się na zagadnieniach niższego rzędu. Na przykład na tym, ile gotówki będziemy potrzebować w danym roku, jakie powinniśmy mieć zapasy itd. Zresztą, wiadomości te są tak czy inaczej potrzebne, wręcz konieczne - choćby po to, by zaplanować proces produkcyjny.

Niżej przedstawimy kilka modeli prognozowania zapotrzebowania na aktywa obrotowe. Nie są one zbyt skomplikowane - i zapewne opisują tylko podstawowe zależności. Mogą jednak stanowić punkt wyjścia do dalszych rozważań.

Bazować będziemy przede wszystkim na pracy A. Szpulak (por. bibliografia), ale także na innych pozycjach.

Przypomnijmy, czym są aktywa obrotowe. Otóż jest to majątek, co do którego sądzimy, iż może zostać upłynniony (przekształcony na gotówkę) stosunkowo szybko. Naturalnie najbardziej płynna jest czysta gotówka w kasie czy na koncie. Jej nie trzeba w ogóle upłynniać, wystarczy ją pobrać. Zalicza się ona do inwestycji krótkoterminowych, które jednak stanowią szerszą kategorię. To również akcje, udziały czy udzielone pożyczki - przy czym zakłada się, że instrumenty te albo mają termin wymagalności krótszy niż 12 miesięcy, albo są przeznaczone do zbycia w ciągu najbliższych 12 miesięcy.

Mniej płynne są należności krótkoterminowe (do 12 miesięcy od dnia bilansowego), przy czym są one obarczone zawsze pewnym ryzykiem. Ostatecznie bywa przecież tak, że kontrahent nam nie płaci... w terminie lub w ogóle.

Zapasy (tj. materiały, półprodukty i produkty w toku, towary, zaliczki na dostawy) to najmniej płynna część aktywów obrotowych. Co prawda mamy do nich raczej prosty dostęp, ale nie zawsze można je szybko sprzedać (zwłaszcza za dobrą cenę).

A zatem, podsumowując: majątek obrotowy to inwestycje krótkoterminowe, należności krótkoterminowe i zapasy, a dodatkowo także krótkoterminowe rozliczenia międzyokresowe.

*

Przedstawmy teraz, w ślad za A. Szpulak, model prognostyczny zapasów materiałowych. Chodzi o materiały, które stosujemy w produkcji naszych własnych wyrobów.

Pierwszy wzór jest taki:

Otóż M_t to dzienne (na dzień t) zapotrzebowanie na materiał do produkcji. Mowa o jego wartości, zatem wielkość wyrażona jest w walucie (w zł). Z kolei Q_t to dzienna produkcja (liczba wytworzonych jednostek). Przez n rozumiemy normę zużycia materiału na jednostkę produkcji, a przez c - jednostkową cenę materiału.

Tak więc dzienne zapotrzebowanie ma materiał można obliczyć stosunkowo prosto. Bardziej złożone jest wyznaczenie zapasu gwarancyjnego (ozn. D₀) i cyklu dostaw (T^D). Tym, jak to zrobić, nie będziemy się tu zajmować; niemniej niektóre informacje znaleźć można w innym naszym tekście nt. gospodarowania zapasami.

Przyjmujemy zatem, że D₀ i T^D są znane. Taki cykl dostaw może wynosić np. 10, 14 albo 30 dni - oznacza to, że co 10, 14 albo 30 dni przychodzą do nas nowe materiały.

Interesuje nas obliczenie wielkości k-tej dostawy. Na przykład, jeśli cykl T^D = 7 (dni), to wielkość zamówienia złożonego w pierwszym dniu będzie sumą zapotrzebowania na materiały do produkcji, które będą wykorzystane w siedmiu kolejnych dniach:

D₁ = M₁ + M₂ + ... + M₇

Kolejne wartości M_t mogą być takie same, a mogą być różne (zmiany produkcji w kolejnych dniach). W każdym razie po siódmym dniu składamy nowe zamówienie (przyjmujemy tutaj, że jest ono od razu realizowane, pomijamy np. czas dostarczenia materiałów do naszej firmy):

D₂ = M₈ + M₉ + ... + M₁₀

Ogólnie wzór będzie mieć następującą postać:

Teraz możemy ustalić poziom zapasów z k-tej dostawy w chwili t:

Jak widać, pojawia się tu zapas gwarancyjny, który zawsze chcemy mieć. Dodajemy do niego wartość k-tej dostawy i odejmujemy wartość tych materiałów, które zostały już zużyte.

Na przykład:

Z_9,2 = D₀ + D₂ - (M₈ + M₉)

*

Teraz przejdziemy do prognozowania należności. Tutaj w miejsce T^D wprowadzamy T^N - tj. cykl inkasowania należności. Znów może to być np. 14, 21 czy 60 dni.

Przyjmijmy dla przykładu, że T^N = 7, czyli każdy kontrahent płaci nam po 7 dniach od wzięcia naszego produktu. W finale siódmego dnia stan należności jest taki:

N₇ = P₁ + ... + P₇

Przez P_i należy rozumieć przychody z i-tego dnia (których nie należy mylić z gotówką - tę dopiero mamy otrzymać). Tak więc nasze przychody to na razie tylko należności. Ale ósmego dnia spłacane są należności z dnia pierwszego; dziewiątego z drugiego itd. Czyli:

N₉ = P₁ + P₂ + ... + P₇ - P₁ - P₂ + P₈ + P₉

Takie rozważania prowadzą nas do wzoru ogólnego:

Należy przy tym pamiętać, że dzienne przychody ze sprzedaży to po prostu iloczyn planowanej dziennej produkcji oraz ceny jednostkowej:

Wróciliśmy tu do indeksu t, w poprzednim wzorze - z uwagi na jego kompozycję - stosowaliśmy i. Naturalnie założenie, iż produkcja się sprzeda i przyniesie przychód... to uproszczenie.

*

My czekamy na należności, ale sami spłacamy zobowiązania. Wypada więc, choć są one pasywami, a nie aktywami, rzec parę słów o ich modelowaniu.

Mówimy o zobowiązaniach z tytułu dostaw i usług. W zasadzie ograniczamy się nawet do zobowiązań z tytułu dostaw, o których była mowa na początku. Takie zobowiązanie powstaje w tym dniu, w którym następuje dostawa materiału. Spójrzmy na poniższą formułę:

Mówi ona, że jeśli np. mamy dzień t = 15, a cykl dostaw wynosi 7, to dostawę z owego dnia 15-tego możemy utożsamić z dostawą D₃, gdyż: jeśli k = 3, to (k-1)*T^D + 1 = (3-1)*7 + 1 = 15 = 5. Faktycznie, pierwszą dostawę mieliśmy w dniu t = 1, drugą po siedmiu dniach, w dniu t = 8, trzecią znów po siedmiu - w dniu t = 15. Zgadza się.

Chodzi o to, że tak naprawdę dostawy następują co jakiś czas, raczej nie codziennie - ale musimy w jakiś "sztuczny" sposób określić pojęcie dostawy na dzień dowolny. Dlatego też opcja trzecia w naszej formule to po prostu zero: np. gdy t = 11, zaś T^D = 7, to t jest różne od 1 i t jest różne od każdego (k-1)7 + 1, przy założeniu, że k to liczba całkowita nie mniejsza niż 1. Innymi słowy, w dniu 11-tym nie ma dostawy, co zapisujemy jako dostawę zerową.

Ale po co to wszystko? Przyjmijmy teraz, że cykl dostaw to 7 dni, a cykl regulacji zobowiązań to 10 dni. To ostatnie znaczy, że zobowiązania spłacamy 10 dni po ich zaistnieniu (a nie, że spłacamy je co 10 dni). Należy przy tym zaznaczyć, że dostawy ujmowane są w księgach w dniu następnym.

Stan zobowiązań oznaczymy literą L. Otóż:

L₇ = D₁ + ... + D₇

Tak naprawdę tylko D₁ jest niezerowa, w kolejnych dniach dostawy są zerowe. A teraz:

L₈ = D₁ + ... + D₈

Zaksięgowano tu D₈, tj. drugą niezerową, faktyczną dostawę. Wiąże się z nią zaciągnięcie odpowiedniego zobowiązania. Na razie żadne zobowiązanie nie zostało uregulowane.
 
Przeskoczmy teraz do dnia 10:

L₁₀ = D₁ + ... + D₈ + D₉ + D₁₀ - D₁

W dniu 10 regulujemy płatność za dostawę z dnia pierwszego, tj. D₁. Czyli zobowiązania maleją o D₁. W międzyczasie "otrzymaliśmy" też (zerowe) dostawę D₉ i D₁₀.

Sprawdźmy stan w dniu 18, wypisując tylko dostawy niezerowe:

L₁₈ = D₁ + D₈ - D₁ + D₁₅ - D₈

Można to opisać tak: w dniu 1 otrzymaliśmy D₁ (i zaciągnieliśmy zobowiązanie w związku z tym pakietem). W dniu 8 otrzymaliśmy drugą dostawę niezerową, tj. D₈. W dniu 10 spłaciliśmy D₁, a w 15-tym otrzymaliśmy nowy transport. Jeszcze za niego nie zapłaciliśmy, ale wczoraj (w dniu 17-tym) uregulowaliśmy dostawę D₈.

Kontynuując takie dywagacje, wyprowadzamy wzór ogólny:

Formuła ta mówi nam, jaki będzie stan zoboiązań w dniu t - w zależności od tego, czy t jest mniejszy od cyklu regulacji zobowiązań, czy też większy / równy.

*

Przedstawmy jeszcze jedną formułę - na poziom środków pieniężnych w momencie t:

Przez CF_t⁺ rozumiemy wpływy w czasie t, CF_t^- to oczywiście wydatki (ubytek gotówki), a G₀ to stała rezerwa gotówki, którą chcemy zachować.

Oczywiście wpływy i wydatki nie biorą się znikąd. Wyrażają się następującymi wzorami:

Jak widać, wpływy z danego dnia równe są przychodom z momentu t - T^N + 1. Innymi słowy, w dniu t otrzymujemy zapłatę, za to, co sprzedaliśmy w okresie t - T^N + 1. Na przykład jeśli należności są regulowane po 14 dniach, to w dniu 17 otrzymujemy gotówkę za dzień 4. Wydatki są z kolei równe dostawom z odpowiedniego dnia, tj. z momentu t - T^L + 1.

Ustaleniu optymalnego poziomu środków pieniężnych poświęciliśmy też odrębny tekst, którego lekturę polecamy.


Adam Witczak


BIBLIOGRAFIA:

M. Dobija, Rachunkowość zarządcza i controlling, PWN 1997

J. Kitowski, Metodyczne aspekty pomiaru cyklu konwersji gotówki w przedsiębiorstwie, Zeszyty Naukowe SGGW w Warszawie - Ekonomika i Organizacja Gospodarki Żywnościowej, r. 2011, nr 88.

A. Szpulak, "Prognozowanie w zarządzaniu aktywami przedsiębiorstwa", Zeszyty Naukowe Uniwersytetu Ekonomicznego w Katowicach, nr 76 (2012)