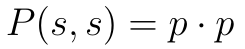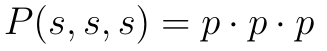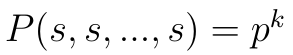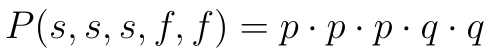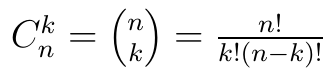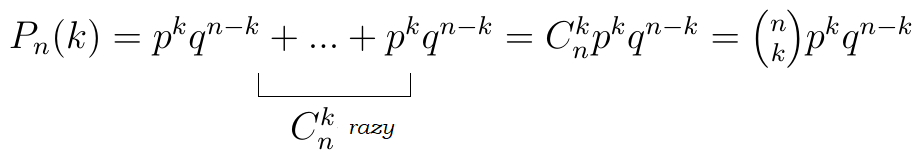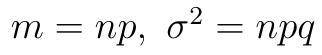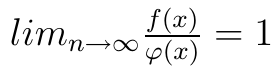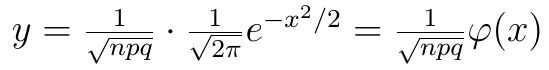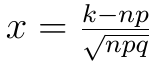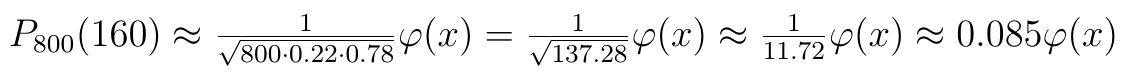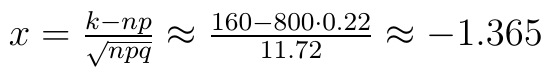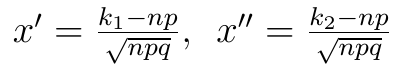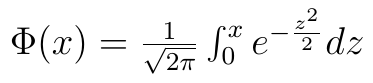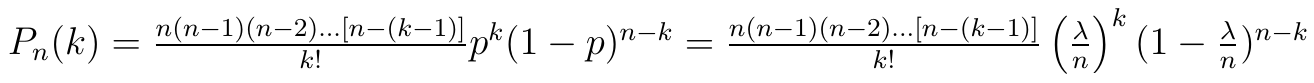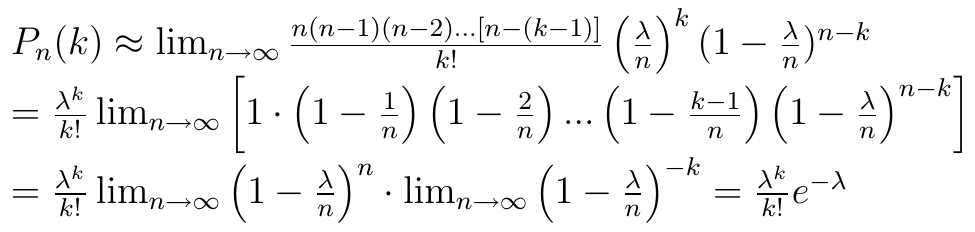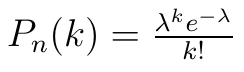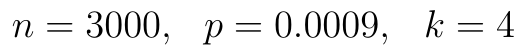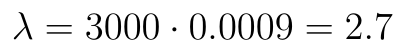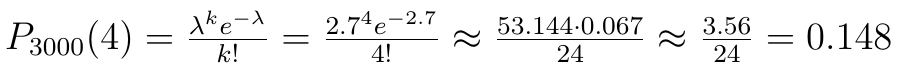Od Bernoulliego do Poissona

Dwumianowy rozkład prawdopodobieństwa zwany jest też rozkładem Bernoulliego - od nazwiska Jakuba Bernoulliego (1654 - 1705), szwajcarskiego fizyka i matematyka. Z nazwą tą wiąże się zresztą pewna kontrowersja. Oto bowiem w krajach anglojęzycznych zwykle mianem Bernoulli distribution określa się rozkład zero-jedynkowy, czyli odnoszący się do pojedynczego doświadczenia Bernoulliego, a nie do ich serii.

Pojedyncze doświadczenie tego typu polega na tym, że zmienna losowa przyjmuje jedną z dwóch wartości: s (tzw. sukces) lub f (tzw. porażkę). Sukces osiągany jest z prawdopodobieństwem p, porażka z prawdopodobieństwem q. Na przykład przy rzucie monetą mamy w zasadzie p = q = 1/2.

Wyobraźmy sobie teraz, że wykonujemy n tego typu niezależnych doświadczeń. Zakładamy, że prawdpodobieństwa sukcesu i porażki są zawsze takie same. Jakie jest prawdopodobieństwo dwóch sukcesów w dwóch próbach? Zgodnie z tym, co wiemy o prawdpodobieństwach zdarzeń niezależnych, wynosi ono:

Dla trzech sukcesów w trzech próbach mamy:

Wzór na prawdopodobieństwo k sukcesów przyjmie zatem następującą postać:

A jeżeli wykonujemy pięć prób i interesuje nas sytuacja, w której są trzy sukcesy i dwie porażki? Wtedy wygląda to jak poniżej:

Uogólnijmy powyższą formułę. Mamy n prób, w tym k sukcesów i w takim razie n-k porażek. Spójrzmy:

Wydaje się to przekonujące, ale zauważmy, że rozważyliśmy tu tylko jeden, konkretny ciąg: s, s, ..., s (k razy), q, q, ..., q (n-k razy). Jeżeli jednak nie martwi nas kwestia kolejności, to godzimy się na to, że sukcesy i porażki będą następować w innej kolejności: ważne jedynie, by pierwszych było k, drugich n-k.

Otóż takich ciągów sukcesów i porażek jest...

To tzw. kombinacje k elementów wybieranych spośród wszystkich n elementów zbioru. Te kombinacje (zdarzenia) wyłączają się wzajemnie, zatem stosujemy twierdzenie o dodawaniu prawdopodobieństw wyłączających się zdarzeń. Trzeba je dodać do siebie C_n^k razy, czyli przemnożyć przez C_n^k (bo każdy z tych ciągów ma takie samo prawdopodobieństwo). Innymi słowy, fakt, że nie interesuje nas kolejność, a jedynie liczba sukcesów i porażek, zwiększa nasze szanse.

Ostatecznie osiągamy następującą formułę:

Rozkład ten to właśnie rozkład dwumianowy (binomial). Ma on wartość oczekiwaną i wariancję określone według następujących wzorów:

Przykład 1.
Prawdopodobieństwo, że poziom promieniowania radioaktywnego na terenie zakładu przekroczy normę w czasie dnia roboczego, wynosi 0.68 (tj. 68 proc.). Jak duża jest szansa, że w ciągu 5 następnych dni poziom promieniowiania 3 razy przebije normę?

Poniżej widzimy podsumowanie danych oraz rozwiązanie zagadnienia przy pomocy schematu Bernoulliego:

Okazuje się, że wynik to ok. 0.32, czyli mniej więcej 32 proc.

*

Jeśli n jest duże, tzn. jeżeli wykonujemy wiele prób (np. 200 albo 1000), to stosowanie tego wzoru okazuje się problematyczne, szczególnie przy ręcznych obliczeniach - głównie dlatego, że trzeba wyliczać silnie z dużych liczb. Dlatego stosuje się inne metody - przybliżone. Jedną z nich jest funkcja asymptotyczna z lokalnego twierdzenia Laplace'a.

Ogólnie rzecz biorąc, funkcję φ(x) nazywamy asymptotycznym przybliżeniem funkcji f(x), gdy zachodzi warunek:

A teraz czas na teoremat:

Twierdzenie (lokalne) Laplace'a.
Jeśli prawdopodobieństwo p zajścia zdarzenia s (sukcesu) w każdym doświadczeniu jest stałe, a zarazem niezerowe i różne od 1, to prawdopodobieństwo P_n(k) tego, że w n doświadczeniach suckes zdarzy się dokładnie k razy, w przybliżeniu równe będzie wartości następującej funkcji:

gdzie

Naturalnie, q = 1 - p, tak jak to było wcześniej. Jeżeli mówimy, że prawdopodobieństwo jest "równe w przybliżeniu" to oznacza to tyle, że rośnie wraz ze wzrostem liczby n: tak jak w ogólnym wzorze obrazującym sens pojęcia funkcji asymptotycznej.

Wartości funkcji φ(x) są podane w tablicach. Jest to funkcja parzysta, zatem φ(-x) = φ(x). W istocie ta funkcja to nic innego, jak gęstość standardowego rozkładu normalnego.

Przykład 2.
Szansa, że pojedyncze doświadczenie zakończy się sukcesem, wynosi 0.22. Jakie jest prawdopodobieństwo, że w trakcie 800 doświadczeń uzyskamy 160 sukcesów?

Podsumujmy dane:

Stosujemy zaprezentowany wcześniej wzór z lokalnego twierdzenia Laplace'a:

Trzeba teraz obliczyć wartość x:

Wspominaliśmy, że wartości funkcji φ są stablicowane. Oczywiście to prawda, ale w dzisiejszych czasach można po prostu posłużyć się komputerem (choćby dlatego, że tablice nie obejmują wszystkich wartości, a tylko niektóre). W języku R możemy wywołać funkcję dnorm(x), która przedstawi nam szukaną wartość. Właśnie z tego narzędzia skorzystaliśmy, by dokończyć obliczenia:

Szukane prawdopodobieństwo to ostatecznie 0.013 (czyli 1,3 proc.). Zauważmy, że jest ono dużo niższe niż szansa w jednym doświadczeniu, wynosząca 0.22. Możemy też przywołać dane z przykładu Gmurmana (por. bibliografia): n = 400, k = 80, p = 0.20, q = 0.80. Finalny wynik to 0.04986, czyli ok. 5 proc. - też dużo mniej niż 20 proc. dla jednego eksperymentu.

Dodajmy, że jeszcze, że pomijamy dowód lokalnego twierdzenia Laplace'a, tak samo jak pominiemy dowód kolejnego twierdzenia imienia tego autora. Powodem jest po prostu to, że dowody te są zbyt skomplikowane, by je tu prezentować.

*

Sytuacja może być bardziej skomplikowana. Przypuśćmy, że pytamy o to, jaka jest szansa, że w n doświadczeniach sukces zdarzy się nie mniej niż k₁ razy i nie więcej niż k₂ razy. O tym mówi kolejne twierdzenie.

Twierdzenie integralne (całkowe) Laplace'a.
Jeśli prawdopodobieństwo p zajścia zdarzenia s (sukcesu) w każdym doświadczeniu jest stałe, a zarazem niezerowe i różne od 1, to prawdopodobieństwo P_n(k₁, k₂) tego, że w n doświadczeniach suckes zdarzy się od k₁ do k₂ razy, w przybliżeniu będzie określone poniższą formułą:

gdzie

Wartości funkcji Φ(x), tzn. następującej:

są podane (dla wybranych x) w tablicach, dołączanych do podręczników. Zauważmy jednak, że Φ(x) uwzględnia całkę jedynie od 0 do x. Nie jest to jednak duży problem, gdyż wcześniejszy wzór można po prostych przekształceniach rozumieć tak:

Wypada jeszcze ujawnić jeden fakt: Φ(x) to po prostu dystrybuanta standardowego rozkładu normalnego.

*

Okazuje się, że choć wzór Laplace'a rozwiązuje w pewnej mierze problem wysokich wartości n, to jednak okazuje się mało przydatny przy bardzo małych prawdopodobieństwach sukcesów: takich, że p nie przekracza 1/10.

Zajmijmy się tym problemem, przyjmując założenie, że iloczyn np jest stały - i oznaczony symbolem λ. Innymi słowy, im więcej prób w naszym modelu, tym mniejsza musi być szansa pojedynczego sukcesu, by utrzymać np jako constans.

Przypomnimy teraz wzór na prawdopodobieństwo k sukcesów w n próbach (tj. wzór rozkładu wielomianowego), uwzględniając wprowadzenie λ:

Formułę tę można dalej przekształcać:

Wyrażenie, które otrzymaliśmy na końcu, określa nam tzw. rozkład Poissona - od nazwiska S. D. Poissona (1781 - 1840), francuskiego matematyka i fizyka. Uwypuklimy tę formułę w osobnej linijce, dla wygody stosując zwykłą równość, a nie przybliżoną (choć to nieścisłe):

Mówi się często, że jest to rozkład prawdopodobieńswa zdarzeń masowych, ale rzadkich (n duże, p małe). Dobrze opisuje on takie zjawiska jak np. liczba awarii w systemach technicznych. Jego pozytywną cechą jest to, że ma tylko jeden parametr, czyli właśnie λ.  

Przykład 3.
Fabryka wysyła do dostawcy 3 tys. sztuk produktu. Podczas transportu jedna sztuka może ulec uszkodzeniu z szaną równą 0.0009. Ile wynosi prawdopodobieństwo, że z nadesłanej partii 4 sztuki będą uszkodzone?

Podsumujmy dane:

Obliczamy wartość λ:

Teraz przechodzimy do obliczenia szukanego prawdopodobieństwa przy pomocy wzoru Poissona:

Wynik, jak się okazuje, to w przybliżeniu 0.148 - tj. ok. 14,8 proc. Być może większy niż mogłoby się wydawać na podstawie wiedzy o szansie uszkodzenia pojedynczego wyrobu? Znów możemy przywołać dane Gmurmana: n = 5000, p - 0.0002, k = 3. Wynik w takim układzie to 0.06.


Adam Witczak

BIBLIOGRAFIA:

W. J. Gmurman, "Rachunek prawdopodobieństwa i statystyka matematyczna", WNT 1975.

W. Ostasiewicz, "Propedeutyka probabilistyki", Wyd. Akademii Ekonomicznej we Wrocławiu 2000.

J. Woch, "Statystyka procesów transportowych", Wyd. Politechniki Śląskiej, Gliwice 2001.