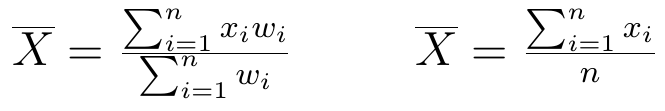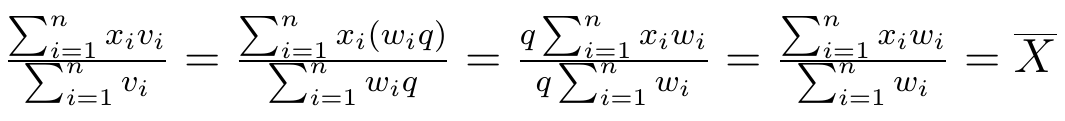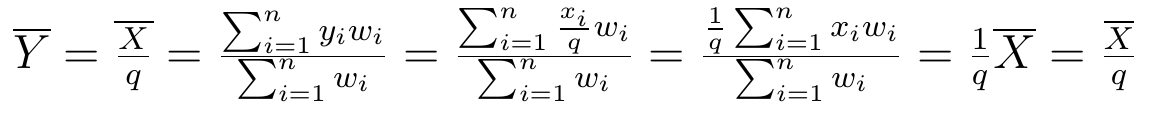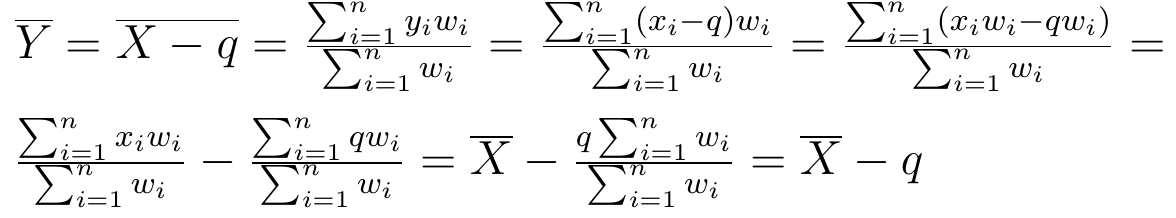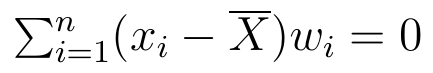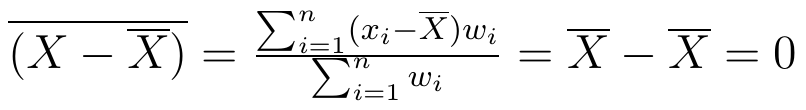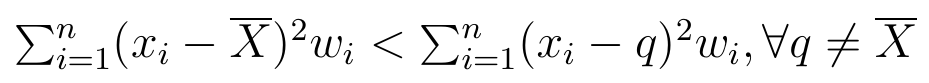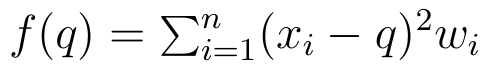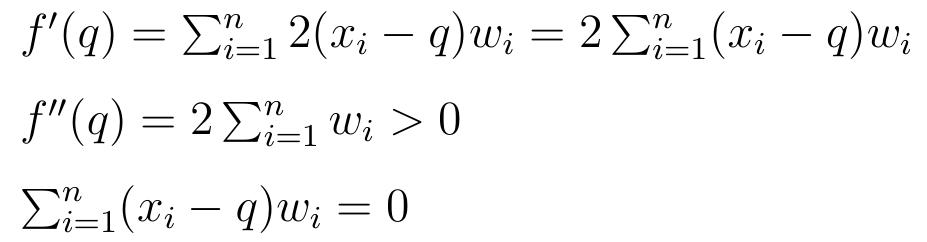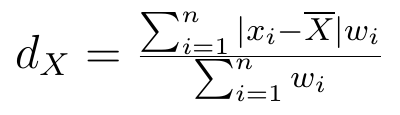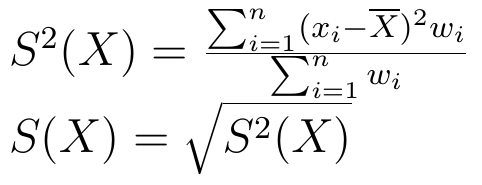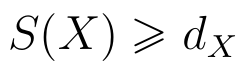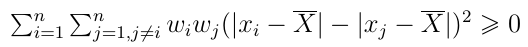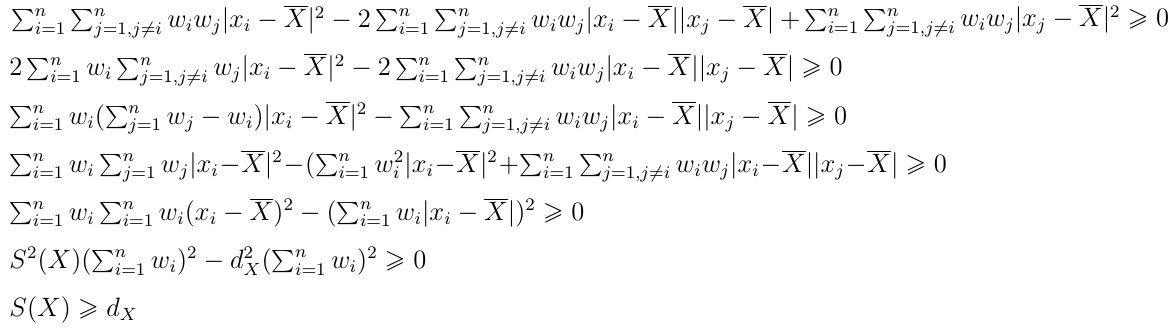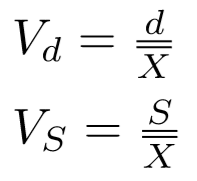Tajniki średniej arytmetycznej

Kiedy używamy w języku potocznym pojęć takich jak "średnia" czy "średnio", to zwykle mamy na myśli albo coś nieokreślonego (i liczymy na to, że nikt nas nie poprosi o doprecyzowanie zagadnienia) - albo średnią arytmetyczną.

To właśnie narzędzie uznajemy odruchowo za dobre do przybliżania czy ujednolicania wielu zjawisk - wielu wielkości - z którymi mamy do czynienia. Przeciętny wzrost sportowca w drużynie, średnia z ocen semestralnych - i przeciętna wypłata w fabryce albo w całym państwie... Te budzące zadumę trzy kropki na końcu poprzedniego zdania to nie przypadek: oto bowiem przy średnim wynagrodzeniu nierzadko obrażamy się na nasze podstawowe narzędzie. Ponieważ średnia arytmetyczna jest wrażliwa na wartości skrajne, to w ostatnich latach coraz częściej mówi się, że np. GUS-owska informacja o przeciętnym wynagrodzeniu za dany miesiąc jest niezbyt miarodajna. Lepiej mówić o dominancie lub medianie zarobków. Dominanta to wartość występująca najczęściej. Mediana - to tak, że połowa Polaków zarabia mniej od niej, a połowa więcej. Obie te kwoty okazują się dużo niższe niż zwykła średnia arytmetyczna. Tę ostatnią zawyża nieliczna grupa pensji ekstremalnie wysokich.

Tak naprawdę nie ma jednoznacznego kryterium, które mówiłoby, jaka funkcja matematyczna jest najlepszą "średnią". Wszystko zależy od tego, jakie mamy dane i czego chcemy się dowiedzieć. W tym artykule nie będziemy zajmować się innymi średnimi niż arytmetyczna, przypomnijmy więc tylko dla porządku, iż rozważa się też średnią harmoniczną i geometryczną, a także przeciętne pozycyjne: jak właśnie dominanta czy mediana. Uogólnieniem pojęcia mediany jest, jak wiadomo, kwantyl.

Co do średniej arytmetycznej, to teoretycznie każdy wie, jak ją obliczyć w najprostszej formie (wystarczy zsumować dane i podzielić przez ich liczbę: stąd (a+b)/2 i (a+b+c)/3). My jednak zaprezentujemy pewne własności średniej, które albo są mniej znane, albo mniej oczywiste, albo są znane i używane, ale niekoniecznie pamięta się przy tym, jak wyglądają dowody ich prawdziwości. Te właśnie dowody (przeliczenia, na ogół krótkie, ale nie zawsze...) zaprezentujemy. Mogą się przydać zwłaszcza studentom i praktykom, pracującym z nowymi wariantami starych formuł.

*

Zasadniczo zakładamy, że rozważamy pewien skończony pakiet danych o charakterze liczbowym; np. x₁, x₂, ..., x_n. Jest ich więc n. Może być tak, że wszystkie uważamy za jednakowo ważne, ale zdarza się, że z pewnych przyczyn liczbom tym nadajemy różne wagi. Na przykład uważamy, że ocena z matematyki jest dwa razy ważniejsza od oceny z plastyki. Wówczas, jeśli uczeń otrzymał 3 z matematyki i 6 z plastyki, to średnia wynosi nie (3+6)/2 = 4.5, ale (2*3 + 1*6)/3 = (6+6)/3 = 4.0. Proszę zauważyć, że w mianowniku mamy sumę wag, tj. 2+1 = 3. Ostatecznie więc uczeń o takich ocenach nie będzie zadowolony z wprowadzenia takich wag: przypisuje mu się średnią 4.0, a nie 4.5.

Zapiszmy rozważane wzory w sposób ogólny:

Po lewej stronie mamy formułę uwzględniającą (różne) wagi (ozn. w_i), po prawej zaś taką, w której wszystkie wagi są takie same, więc można je pominąć. Istotnie, gdyby zarówno matematyka, jak i plastyka miały wagi równe 2, to w poprzednim przykładzie mielibyśmy (2*3 + 2*6)/(2+2) = 18/4 = 4.5, czyli tyle samo, co przy wagach 1 i 1.

Dla formalności możemy przyjąć, że nasze dane to pewna zmienna X (np. wiek, wzrost, ocena etc.), która przyjmuje konkretne wartości (np. w czasie, jak w przypadku temperatury zmieniającej się w pokoju; albo w populacji, jak w przypadku ocen z różnych przedmiotów czy ocen wielu osób z jednego przedmiotu).

Bardzo często jako wagi traktujemy po prostu liczebności. Jeśli np. w ośmioosobowej grupie studentów mamy trzech 20-latków, czterech 22-latków i jednego 25-latka, to można uznać, że wagi wynoszą odpowiednio: 3 (dla liczby 20), 4 (dla 22) i 1 (dla 25). Sumują się one rzecz jasna do 8, tj. do liczby członków grupy. Średnia to (3*20 + 4*22 + 1*25)/8 = (60 + 88 + 25)/8 = 173/8 = 21.625.

Należy dodać, że zawsze zakładamy, iż wagi są nieujemne, a w dodatku przynajmniej jedna jest dodatnia. Inaczej mielibyśmy w mianowniku ułamka liczbę 0.

Teraz, na ogół w ślad za książką B. Szulca, przedstawimy kilka podstawowych własności średniej arytmetycznej:

1) Jeśli wszystkie wagi w_i (i = 1, ..., n) pomnożymy przez tę samą liczbę q, to średnia arytmetyczna nie ulegnie zmianie:

Powyżej mamy odpowiednie przeliczenie, przy czym v_i = w_i*q. Zobaczmy to na przykładzie. Wróćmy do naszej grupy studentów i przyjmijmy, że teraz jest dziewięciu 20-latków, dwunastu 22-latków i trzech 25-latków. Tak więc nasze q równe jest 3 (każda waga została trzykrotnie zwiększona).

Średnia: (9*20 + 12*22 + 3*25)/(9 + 12 + 3) = (180 + 264 + 75)/24 = 519/24 = 21.625.

Oczywiście to tylko przykład: dowód ogólny widzieliśmy wcześniej. Ostatecznie wniosek jest taki: wartość średniej zależy nie od absolutnych wielkości wag, ale od ich proporcji. Tak więc w przykładzie z ocenami istotne było to, że matematyka była dwa razy ważniejsza od muzyki. Wzięliśmy wagi 2 i 1, ale równie dobrze mogliśmy wziąć 1 i 1/2 albo 4 i 2.

2) Jeśli wszystkie wartości zmiennej X podzielimy przez dowolną stałą q, to średnia arytmetyczna nowej zmiennej Y = X/q będzie q razy mniejsza od średniej z X:

Powyżej widzimy dowód tego faktu. Oczywiście działa on także dla przemnożenia liczb przez stałą. Wystarczy przyjąć, że q = 1/p, p różne od zera.

Wyobraźmy sobie, że nasi studenci mają teraz 10, 11 i 12.5 roku, a proporcje liczebności są nadal 3:4:1.

Zatem średnia to: (3*10 + 4+11 + 1*12.5)/8 = 86.5/8 = 10.8125. Ale 10.8125 = 21.625/2. W rzeczywistości mogliśmy od razu zastosować udowodniony wzór, przyjmując q = 2 (dzielenie przez dwa). Ważne: mówimy tu o mnożeniu i dzieleniu danych, a nie wag!

3) Jeżeli od wszystkich wartości zmiennej X odejmiemy dowolną stałą q, to średnia arytmetyczna nowej zmiennej Y = X - q będzie mniejsza o q od wyjściowej średniej:

Przeliczenie tego nie jest trudne. Naturalnie można przyjąć q = -p dla dowolnego p i wówczas powyższe twierdzenie można sformułować w kontekście dodawania, a nie odejmowania.

Przykład: obniżmy o 2 lata wiek naszych studentów, niech będzie teraz trzech 18-latków, czterech 20-latków i jeden 23-latek. Średnia to: (3*18 + 4*20 + 1*23)/8 = 19.625. Ale to jest 21.625 - 2. Oczywiście spodziewaliśmy się tego, znając już ogólną formułę.

4) Suma ważonych odchyleń wartości zmiennej X od średniej arytmetycznej wartości tej zmiennej jest zawsze równa zero. To znaczy:

Najpierw zobaczmy to na przykładzie, znów korzystając z naszych ośmiu wiernych studentów: 3(20 - 21.625) + 4(22 - 21.625) + 1(25 - 21.625) = -4.875 + 1.5 + 3.375 = -4.875 + 4.875 = 0.

Nie jest to wcale takie oczywiste. Dowód jest krótki, ale to dlatego, że korzystamy z równości wykazanej w punkcie 4:

Jak widać, za q podstawiliśmy średnią z X. Ostatnia równość jest możliwa tylko, gdy licznik ułamka jest zerowy - a ten licznik to właśnie wspomniana wcześniej suma (ważonych) odchyleń wartości zmiennej od średniej. Niedługo zobaczymy, jakie znaczenie ma odchylenie od średniej w kontekście tzw. odchylenia przeciętnego.

Zacytujmy jeszcze B. Szulca, który pisze, iż dowiedziona właściwość jest tak charakterystyczna dla średniej arytmetycznej, że bywa używana dla jej zdefiniowania. Można mianowicie określić średnią arytmetyczną wartości zmiennej X jako taką wartość, od której suma ważonych odchyleń wartości zmiennej X jest równa zeru.

6) Suma ważonych kwadratów odchyleń wartości zmiennej X od średniej arytmetycznej wartości tej zmiennej jest mniejsza niż od jakiejkolwiek innej stałej.

Innymi słowy, średnia arytmetyczna minimalizuje sumę (ważonych) kwadratów odchyleń zmiennej X od stałej. Można to zapisać tak:

Ale to jeszcze nie dowód. Otóż dowód korzysta z metod rachunku różniczkowego. Rozważmy funkcję:

Obliczamy jej pierwszą pochodną (względem zmiennej q, rzecz jasna). Następnie liczymy drugą pochodną i stwierdzamy, że jest ona zawsze większa od zera (bo suma wag jest większa od zera). Wreszcie, przyrównujemy pierwszą pochodną do zera.

Z analizy matematycznej: jeśli druga pochodna jest większa od zera, to miejsce zerowe pierwszej pochodnej jest minimum wyjściowej funkcji. Tymczasem trzeci warunek na ostatnim obrazku jest spełniony, jak wiemy z punktu 5), tylko gdy q równe jest średniej z X.

*

W jaki sposób sprawdzić, czy średnia arytmetyczna w miarę dobrze przybliża dane? Przypomnijmy, że odchylenia od średniej sumowały się do zera. A gdybyśmy wzięli pod uwagę wartości bezwzględne tych odchyleń? Jako że są one z samej definicji nie mniejsze niż zero, to taka będzie też ich suma.

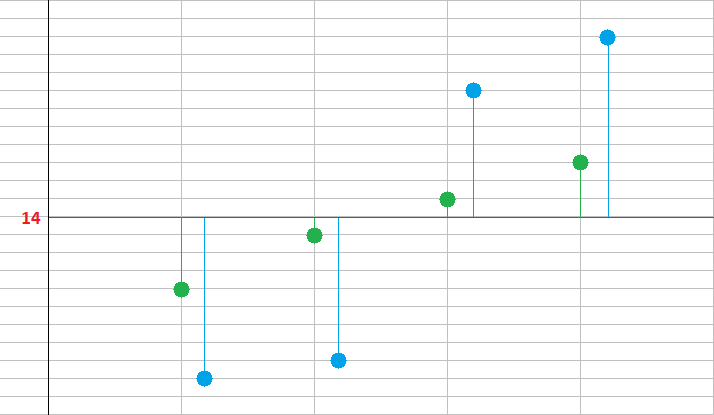
Spójrzmy na poniższy obrazek.

Przedstawia on coś w rodzaju układu współrzędnych, tyle że znaczenie ma dla nas jedynie oś pionowa. Otóż czerwona pozioma półprosta wyznacza nam liczbę 14. Jest to średnia dla dwóch zestawów danych, które rozważamy. To dane "zielone" i "niebieskie". W obu pakietach mamy po 4 liczby. Zielone to 10, 13, 15 i 18. Niebieskie to 5, 6, 21 i 24. Średnia dla obu zestawów to właśnie 14 (mianowicie 56/4).

Odcinki zielone i niebieskie pokazują nam, jak daleko od średniej jest dana wartość. Łatwo zauważyć, że gdybyśmy zsumowali długości wszystkich odcinków zielonych (długości - a więc wielkości dodatnie!), to uzyskalibyśmy liczbę znacznie mniejszą niż po zsumowaniu odcinków niebieskich. Można więc powiedzieć, że w pewnym sensie "niebieskie" liczby są bardziej oddalone od swojej średniej.

Przeliczmy odległości "zielone": 4 + 1 + 2 + 3 = 10. Możemy je podzielić przez ilość danych, tj. przez 4 - by otrzymać coś na kształt średniej arytmetycznej: 10/4 = 2.50.

A teraz odległości "niebieskie": 9 + 8 + 7 + 10 = 34. Dalej: 34/4 = 8.50.

To, co przed chwilą zrobiliśmy to nic innego, jak obliczenie odchyleń przeciętnych (przy założeniu, że wszystkie wagi są jednakowe). Wystarczy spojrzeć na ogólny wzór odchylenia przeciętnego:

Wszystko się zgadza (możemy uznać, że wszystkie w_i były równe 1). Sensowne zdaje się stwierdzenie, że średnia arytmetyczna gorzej przybliża czy obrazuje dane niebieskie niż dane zielone. W obu przypadkach ta średnia to 14. Jeśli mamy 10-latka, 13-latka, 15-latka i 18-latka, to intuicyjnie wydaje nam się w miarę rozsądne stwierdzenie, że były to dzieci mające średnio... no cóż, 14 lat. Ale jeśli mamy 5-latka, 6-latka, 21-latka i 24-latka, to powiedzenie, że przeciętnie mieliśmy do czynienia z 14-latkami wyda nam się cokolwiek dziwne - mimo że formalnie to prawda. Odchylenie danych "niebieskich" jest większe niż danych "zielonych".

Zgodnie z zaprezentowanym wzorem, odchylenie przeciętne wartości zmiennej X definiuje się jako średnią arytmetyczną modułów odchyleń wartości zmiennej X od ich średniej arytmetycznej. A więc mamy tu średnią z wartości bezwzględnych odchyleń od średniej. Im wyższe to odchylenie, tym większe jest rozproszenie zmiennej X - i tym mniej miarodajna jest średnia arytmetyczna.

Weźmy skrajny przykład. Znów 4 odczyty: 1, 2, 3 i 50. Średnia to nadal 56/4 = 14. Ale czy byłoby rozważne mówienie, że przeciętnie mamy tu do czynienia z 14-latkami? Odchylenie przeciętne wynosi: (13 + 12 + 11 + 42)/4 = 19.50. "Średnio" każda liczba jest o 19.5 odchylona od 14...

*

Inna metoda sprawdzania miarodajności średniej arytmetycznej to odchylenie standardowe. Jego konstrukcja jest podobna do przeciętnego - ale zamiast modułów bierzemy kwadraty różnic:

S² nazywamy wariancją, zaś pierwiastek z wariancji to właśnie odchylenie standardowe. Ponieważ mamy kwadraty, czyli liczby z natury rzeczy nieujemne, to znów unikamy wyzerowania się odchyleń.

Na przykład dla danych "zielonych" odchylenie standardowe to pierwiastek z ((10-14)^2 + (13-14)^2 + (15-14)^2 + (18-14)^2)/4 = (16 + 1 + 1 + 16) = 34/4. Czyli pierwiastek z 8.50, a to jest ok. 2.91.

Dla danych "niebieskich" mamy pierwiastek z ((5-14)^2 + (6-14)^2 + (21-14)^2 + (24-14)^2)/4, tj. pierwiastek z (81 + 64 + 49 + 100)/4, więc pierwiastek z 73.5, a to jest ok. 8.57.

W obu przypadkach odchylenie standardowe okazało się większe od przeciętnego. Okazuje się, że to ogólna, matematyczna właściwość:

Zazwyczaj na tym się poprzestaje, przynajmniej w książkach dla ekonomistów czy inżynierów. Także i my traktujemy dowód nierówności jako coś zupełnie dodatkowego, stąd zaprezentujemy go mniejszą czcionką. Pół żartem, pół serio, jest to lektura nadobowiązkowa. Punkt wyjścia to poniższa nierówność:

Nie wnikamy w to, jak wpaść na to, żeby zacząć właśnie od niej. W każdym razie jest ona zawsze prawdziwa, bo sumowane są nieujemne czynniki. Równość jest możliwa tylko, gdy x_i = x_j dla wszystkich i,j - a zatem, gdy wartość zmiennej w ogóle nie jest zróżnicowana, czyli n razy powtarza się ta sama liczba (np. 5, 5, 5, 5, 5).

Przekształcenia wyjściowej nierówności wyglądają następująco:

Nie będziemy ich omawiać w detalach. Dość rzec, iż na początku wykorzystujemy wzór skróconego mnożenia, a potem fakt, iż pierwszy i ostatni wyraz pierwszego wiersza są sobie równe (liczenie wyrazów x_i i x_j to przecież to samo, to jedynie kwestia indeksowania).

Finalnie wszystko jest przekształcone tak, że dostajemy oczekiwaną nierówność.

*

Odchylenia przeciętne i standardowe wyrażone są w liczbach, które mają pewien kontekst. Nie zawsze potrafimy powiedzieć od razu, czy np. odchylenie równe 5.25 jest duże czy małe. Jeśli średnia będzie wynosić 2350, to raczej bardzo małe, a jeśli 1.25 - to raczej bardzo duże... Niemniej przydałoby się to jakoś ujednolicić. W tym celu wprowadza się tzw. współczynniki zmienności:

Pierwszy - V_d - jest powiązany z odchyleniem przeciętnym. Drugi - V_S - ze standardowym. Oba to iloczyny odpowiednich odchyleń i średniej arytmetycznej. Wynik zostaje zatem ujednolicony do pewnej proporcji, którą na ogół wyraża się w procentach.

I tak np. dla naszych danych "zielonych":

V_d = 2.50/14 = 17.8 proc., V_S = 2.91/14 = 20,8 proc.

Dla "niebieskich":

V_d = 8.50/14 = 60,7 proc., V_S = 8.57/14 = 61.2 proc.

Wyniki podaliśmy w formie przybliżonej. Zmienność danych "niebieskich" jest dużo większa niż zmienność "zielonych", to ok. 60 proc. Co więcej, możemy teraz porównywać zmienności danych z zupełnie innej skali. Weźmy np. taki pakiet (oczywiście nie ma nic złego w tym, że bierzemy teraz więcej danych, równie dobrze moglibyśmy znów poprzestać na jakichś czterech liczbach): 3950, 4000, 4120, 4150, 4290, 4400. Średnia tych sześciu liczb to 24910/6 = ok. 4151.7. Odchylenie przeciętne wynosi w przybliżeniu (201.7 + 151.7 + 1.7 + 138.3 + 248.3)/6 = 741.7/6 = 123.6. Trudno to porównać z naszymi danymi "zielonymi" i "niebieskimi". Zupełnie inna skala. Liczymy więc V_d = 123.6/4151.7 = 2.98 proc. To bardzo małe rozproszenie, dużo mniejsze niż w przypadku danych "zielonych", o "niebieskich" nie wspominając.

Adam Witczak

BIBLIOGRAFIA:

"Metody statystyczne w zarządzaniu", pod red. D. Witkowskiej, Wydział Organizacji i Zarządzania Politechniki Łódzkiej 1999.

"Wspomaganie procesów decyzyjnych. Tom I. Statystyka", pod red. M. Lipiec-Zajchowskiej, C.H. Beck 2003.

B. Szulc, "Statystyka dla ekonomistów", Państwowe Wydawnictwo Ekonomiczne 1969.