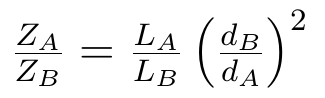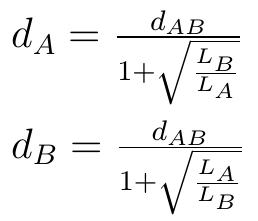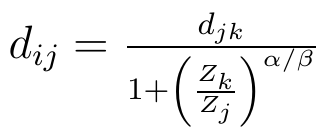Prawo grawitacji detalu Reilly'ego

Prawa ekonomiczne są niestety słabsze od praw fizyki, nie mówiąc już o twierdzeniach matematycznych. Słabsze w tym sensie, że oparte na znacznie bardziej kruchych podstawach i podatne na różnego rodzaju odchylenia, wynikające ze zmian w ludzkiej mentalności, w rozwoju technologicznym, w polityce gospodarczej państwa, a nawet w klimacie czy wręcz pogodzie.

Oczywiście nie mówimy tu o tych prawach, które de facto są matematycznymi tautologiami: jak np. stwierdzenie, że rentowność obligacji na rynku wtórnym rośnie, gdy spada ich cena; albo że zwyżka kursu EUR/USD oznacza spadek kursu pary USD/EUR. Inaczej być nie może: nie robimy tu nic poza przekształcaniem definicji pojęć takich jak 'obligacja', 'rentowność' czy 'kurs pary walutowej'.

Z prawami, które wykraczają poza czysto logiczne i matematyczne przekształcenia, które bazują na obserwacjach ze świata empirycznego, na statystyce lub na pewnych założeniach dotyczących zachowania ludzi - sprawa ma się inaczej. Takie narzędzia jak krzywa Philipsa, cykle makroekonomiczne, krzywa Laffera czy równanie Fishera - nie mają absolutnie uniwersalnego charakteru. O ich sens i zasięg obowiązywania toczą się spory. W grę wchodzą nawet głębokie założenia metodologiczne z obszaru prakseologii i filozofii.

Wspominamy o tym dlatego, by nie nadawać przesadnego znaczenia równaniu, które za chwilę przedstawimy. Jest ono stosowane w różnego rodzaju badaniach rynku czy też analizach marketingowych. To tzw. prawo grawitacji detalu Reilly'ego.

Grawitacja kojarzy się z fizyką - i słusznie. W tym wypadku mamy (tylko i aż) pewną analogię, która bazuje na badaniach empirycznych i określonych założeniach co do ludzkiej psychologii.

Prawo to zostało zaprezentowane przez Williama J. Reilly'ego w pracy "The Law of Retail Gravitation", która ukazała się w roku 1931, a więc blisko 90 lat temu. Na stronie 9. tego dzieła p. Reilly, ekonomista żyjący w latach 1899 - 1970, napisał tak: Two cities attract trade from an  intermediate town in the vicinity of the breaking  point, approximately in direct proportion to the  population of the two cities, and in inverse  proportion to the squares of the distance to the  intermediate towns.

R. Wolny w "Badaniach rynku" pod red. Z. Kędzior formułuje to tak: Prawo grawitacji detalu Reilly'ego mówi, że wielkość zakupów dokonanych w miastach (rejonach) A i B przez mieszkańców położonego między nimi miasta (rejonu) C jest wprost proporcjonalna do liczby ich mieszkańców, a odwrotnie proporcjonalna do kwadratu odległości między nimi.

Wyraża to następująca formuła:

Oznaczenia są takie jak podano niżej:

Z_A - zakupy w mieście A (można to rozumieć jako liczbę "aktów kupna")

Z_B - zakupy w mieście B

L_A - liczba mieszkańców A

L_B - liczba mieszkańców B

d_A - odległość z A do miejscowości pośredniej

d_B - odległość z B do miejscowości pośredniej

Raz jeszcze powtórzmy: jest to model oparty o pewne obserwacje świata rzeczywistego. Innymi słowy, twórca uznał, że to, co widać w życiu gospodarczym, można przybliżyć takim wzorem, który z jakichś powodów się sprawdza. Nie jest to jakaś absolutnie pewna prawda matematyczna. Mogą zaistnieć rynki i społeczeństwa, w których ta proporcja zostanie zaburzona. Jeżeli jednak weźmiemy formułę Reilly'ego za dobrą monetę, to będziemy mogli z góry określić, gdzie np. częściej zakupów dokonuje ludność Kędzierzyna-Koźla: w Opolu czy Gliwicach - dysponując tylko łatwymi do zdobycia informacjami na temat odległości i liczby mieszkańców. Naturalnie można postawić zarzut, że przecież liczby się nie tyle sama odległość, ile np. łatwość dojazdu; że wzór nie uwzględnia tego, iż pewnego rodzaju towarów czy sklepów może nie być w Gliwicach, a są w Opolu (lub odwrotnie). A jednak najwidoczniej w wielu przypadkach równanie się sprawdza. W jakimś sensie można to zrozumieć: mieszkańcy miasta C w zasadzie wolą robić zakupy w miejscowości o dużej liczbie mieszkańców, bo prawdopodobnie jest tam więcej sklepów i lepszy czy też szerszy asortyment; z drugiej strony, zbyt duża odległość może zniechęcać (przy czym zasadniczo proporcja dotyczy kwadratu odległości).

Zresztą, prawda jest taka, że wzór Reilly'ego dotyczy przede wszystkim sytuacji, w której wspomniane wyżej czynniki nie mają znaczenia: zakłada się, że teren jest płaski, miasta podobnie zaopatrzone, brak jest poważnych przeszkód naturalnych, z powodu których dana miejscowość byłaby trudniej dostępna (mimo że formalnie bliższa) - i tak dalej. Jest to więc świat wyidealizowany.

Tak czy inaczej, wzór pozwala na określenie punktu równowagi czy też granicy obojętności. To wąska strefa, której mieszkańcy równie chętnie jeżdżą na zakupy do A, jak i do B. Tak więc na granicy wzór się uprości do nieco trywialnej postaci:

Możemy też określić zasięgi rynków miast A i B, rozważając formułę podaną przed chwilą, przyrównując ją do wyjściowej i dokonując przekształceń, które owocują takimi formułami:

Przez d_AB rozumiemy po prostu odległość pomiędzy miastami A i B.

*

Jak to wszystko wykorzystać w praktyce? Rozważmy następujący przykład, oparty o fikcyjne dane. Mamy dwa miasta: A i B. Pomiędzy nimi znajduje się miasto C: 22 km od A oraz 36 km od B. Przyjmijmy, że w A mieszka 125 tys. ludzi, w B natomiast 165 tys. ludzi. Podstawmy te dane do zaprezentowanego na początku wzoru:

Z_A / Z_B = 165/125 * (36 / 22)^2 = 1.32 * 2.68 = 3.54

Dwie ostatnie równości podaliśmy w formie przybliżonej. W każdym razie rezultat interpretuje się tak: mieszkańcy C chętniej kupują w mieście A niż w B. Mianowicie na każde 100 zakupów w B przypadają ok. 354 zakupy w A.

Jeśli przyjąć, że odległość z A do B to po prostu suma d_A i d_B (co jest uproszczeniem, ale pozostańmy przy tym), wówczas:

d_A = 58/(1 + sqrt(165/125)) = 58 / 2.15 = 27

d_B = 58/(1 + sqrt(125/165)) = 58 / 1.76 = 33

Wyniki podajemy w formie przybliżonej. Oczywiście teraz d_A i d_B to już nie odległości do C, ale do hipotetycznego punktu, którego mieszkańcom jest obojętne, gdzie dokonują zakupów i teoretycznie robią ich tyle samo w A, co w B. Wyszło nam, że ten punkt jest w odległości ok. 27 km od A oraz ok. 33 km od B.

Wzór Reilly'ego można zaprezentować także w postaci bardziej ogólnej:

Co się tu zmieniło? Po pierwsze, zakładamy, że mamy N "miejsc popytu konsumentów", tj. owych miast pośrednich, takich jak poprzednio C. Są one indeksowane literkami i oraz l. Do tego jest M "centrów rynkowych", czyli dużych miast, odpowiedników A i B. Są one indeksowane przez j oraz k. Dalej: Z_ij, Z_ik to ilości zakupów, które mieszkańcy i-tego miasta pośredniego dokonują odpowiednio w j-tym i k-tym centrum, analogicznie należy interpretować d_ij i d_jk (jako odległości do centrów). Co do α i β, to są one wyznaczane empirycznie i teoretycznie mogą być bardzo rozmaite. Jak widzieliśmy, w podstawowej wersji wzorów są one proste: α = 1, β = 1/2 (dlatego też otrzymujemy pierwiastek z ilorazu odległości).

Gdybyśmy teraz przyjęli, że proporcja Zij / Z_ik wynosi 1, a następnie wyliczyli d_ij, czyli odległość punktu równowagi od j-tego centrum, to efektem będzie taki wzór:

Jak widać, jest on podobny do tego, który wynikał z wersji podstawowej, tyle że nasz pierwiastek będzie być bardziej skomplikowany, bo mamy potęgę α/β, niekoniecznie więc pierwiastek kwadratowy.

Adam Witczak


BIBLIOGRAFIA:

"Badania rynku", red. Z. Kędzior, Polskie Wydawnictwo Ekonomiczne 2005

M. Batty, "Reilly's challenge: new laws of retail gravitation which define systems of central places", Environment and Planning A, 1978, volume 10.

W. Friske, S. Choi, "Another Look at Retail Gravitation Theory: History, Analysis and Future Considerations", ABD Journal Volume 5, Number 1, 2013.

W. J. Reilly, "The Law of Retail Gravitation", Pilsbury, New York 1931.