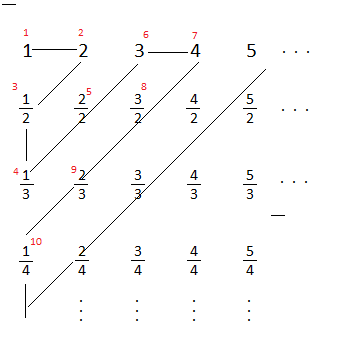
Na powyższym obrazku przedstawiono sposób ponumerowania (małymi czerwonymi liczbami) liczb wymiernych dodatnich (dla uproszczenia sprawy; pamiętajmy przy tym, że zero nie jest liczbą dodatnią). Nie twierdzimy przy tym, że liczba 1 jest "pierwszą" z dodatnich liczb wymiernych w takim np. sensie, w jakim np. jest pierwszą dodatnią liczbą całkowitą. Powyższy obrazek mógłby wyglądać inaczej – istotne jest jedynie to, że pokazaliśmy drogę przy pomocy której każdej liczbie wymiernej (dodatniej) można "nadać numerek" (naturalny). Możemy ustawić wymierne dodatnie w ciąg. Oczywiście dokonując ostatecznego ustawienia usuniemy wszystkie te ułamki, które da się skrócić (licznik i mianownik mają wspólny czynnik) – na przykład skoro mamy 1, to nie będzie nam już potrzebne 2/2 czy 3/3, skoro mamy 3/4, to pominiemy 6/8 i 9/12.

Pójdźmy więc za ciosem i pokażmy, że liczb rzeczywistych również jest dokładnie tyle, ile naturalnych. Niestety, tego uczynić nie możemy – bo tak nie jest. Liczb rzeczywistych nie da się ponumerować. Wykażemy to nie wprost. Na czym polega dowód nie wprost? W gruncie rzeczy często stosujemy w życiu codziennym nie do końca ścisłe, a jednak pożyteczne dowody tego rodzaju. Możemy na przykład powiedzieć: "To niemożliwe, że w tym pokoju odkurzano, bo wtedy na środku dywanu na pewno nie byłoby tych okruchów". Przyjęliśmy, że na dywanie są okruchy (widzimy to) i "na próbę" założyliśmy, że w pokoju odkurzano. Odkrywamy jednak sprzeczność z naszą obserwacją – gdyby odkurzano, to odkurzacz niechybnie wciągnąłby okruchy[1]. A zatem nasze podejrzenie, iż odkurzano – jest błędne, bo kłóci się z tym, co wiemy na pewno. Analogicznie i my pokażemy, że "to niemożliwe, iż liczb rzeczywistych jest tyle samo, co naturalnych – bo wówczas...". Bo wówczas doszlibyśmy do jakiejś sprzeczności, nonsensu, absurdu.

Przez liczby rzeczywiste będziemy rozumieć sumę zbiorów liczb wymiernych i niewymiernych, ale warto znać także definicje formalne. Dwie podstawowe to ta, która bazuje na przekrojach Dedekinda – i ta, którą wprowadził właśnie Georg Cantor. Nie będziemy jednak teraz czynić kolejnej dygresji.

Czytelnik  zgodzi się zapewne, że dowolną liczbę rzeczywistą można zapisać jako ułamek dziesiętny nieskończony, a to mianowicie według wzoru:

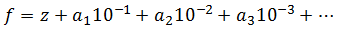
Na przykład możemy mieć 0,333... (czyli jedną trzecią – zakładamy, że tak naprawdę w miejscu kropek powtarzają się w nieskończoność trójki), 0,500... (to po prostu 1/2, zakładamy, że zera też powtarzają się w nieskończoność) albo rozwinięcie dziesiętne liczby pi, którego pierwsze cyfry to 3,1415...

Załóżmy zatem, że w jakiś tajemniczy sposób udało się nam ponumerować liczby rzeczywiste. Zakładamy to nie wprost. Można wyobrazić sobie, że jakiś dobry znajomy zapewnia nas z ogniem w oczach, że przed chwilą udało mu się dokonać tego wyczynu. Wówczas my przedstawiamy mu liczbę niewątpliwie rzeczywistą, a zarazem taką, której z całą pewnością nie udało mu się "przeliczyć", tj. oznaczyć numerem, powiązać z jakąś liczbą naturalną. Mało tego, poprowadzimy rozumowanie w ten sposób, by zagwarantować, że znajomy niczym nas już nie zaskoczy – za każdym razem będziemy mogli powtórzyć rozumowanie, nawet jeśli on w międzyczasie włączy naszą liczbę w swój ciąg.

Właśnie – ciąg. Otóż skoro liczby rzeczywiste można ponumerować, to można ustawić je w ciąg. Pierwsza, druga, setna, milionowa, miliardowa liczba etc. Taki ciąg, zawierający wszystkie liczby rzeczywiste, wyglądałby więc następująco (prezentujemy postać trzech pierwszych wyrazów):

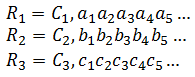Dalej wyglądałoby to analogicznie. Powstałby zatem ciąg rozwinięć dziesiętnych, coś w rodzaju: 0,12443..., 1,353535..., 4,24000... itd. Prędzej czy później ma się w nim rzekomo pojawić każda liczba rzeczywista.

Tworzymy zatem nową liczbę. Jak? Niech będzie to (czysto arbitralne założenie) liczba mniejsza od 1, większa od zera. Co wstawimy po przecinku? Na pierwszym miejscu dowolną cyfrę, która będzie różna od pierwszej cyfry wyrazu R₁ naszego ciągu, czyli od a₁. Niech będzie też różna od 0 i 9 (bo wiemy, że np. 0,999... to w istocie 1,000..., ale chcemy uniknąć dwuznaczności). Przykładowo, jeśli pierwszym wyrazem naszego ciągu jest 2,4536... - to na pierwsze miejsce po przecinku naszej nowej liczby wybieramy dowolną cyfrę inną niż 0, 4 i 9 – np. 3.

Na drugie miejsce wstawiamy dowolną cyfrę różną od b₂ – czyli od tego, co znajduje się w drugim wyrazie ciągu na drugim miejscu po przecinku. Dalej postępujemy podobnie: na trzecie miejsce naszej nowej liczby dajemy cyfrę różną od c₃ – i tak dalej. Ostatecznie powstaje nam liczba wyglądająca tak: N = 0,N₁N₂N₃N₄...

Co można o niej powiedzieć? Z pewnością to, że różni się od każdej z liczb R₁, R₂... Dlaczego? Bo od każdej z nich różni się przynajmniej jedną cyfrą – np. od R₁₀ różni się cyfrą na miejscu dziesiątym (zgodnie z naszym sposobem konstruowania). Co to oznacza? Przypomnijmy, że ciąg R₁, R₂, R₃ ... miał zawierać wszystkie liczby rzeczywiste. Problem w tym, że naszej nowej liczby z pewnością nie zawiera. Wnioskujemy zatem, że nasze (czy też naszego dobrego znajomego) przekonanie, że udało się ponumerować (przeliczyć) liczby rzeczywiste – było złudzeniem. Podaliśmy kontrprzykład dla tezy. Swoją drogą, zbiory, które mają tyle samo elementów, co zbiór liczb naturalnych – nazywamy przeliczalnymi. Zbiór liczb rzeczywistych jest więc nieprzeliczalny.

Faktu tego dowiedziemy także w inny sposób. Wpierw jednak zauważmy, że moc każdego odcinka otwartego (domkniętego, jak się okazuje, też) jest taka sama, jak całego zbioru liczb rzeczywistych. Funkcją, która przeprowadzi nam odcinek na cały zbiór liczb rzeczywistych jest tg(ax) – z odpowiednio dobranym a. Co za tym idzie, aby dowieść czegoś o continuum, tj. mocy zbioru liczb rzeczywistych, wystarczy, że przedstawimy ten fakt na odcinku - np. (0, 1).

Co właściwie chcemy pokazać? Że dla każdego zadanego nam ciągu liczb rzeczywistych z (0, 1)  (oznaczonego np. jako a₁, a₂, a₃ ...) możemy znaleźć taką liczbę c (rzeczywistą), która doń nie należy. Dla każdego – a więc nie ma takiego ciągu, w którym byłyby wszystkie liczby rzeczywiste.

Tym razem robimy to tak. Bierzemy odcinek (0, 1) i budujemy ciąg kolejnych odcinków: (p₁, q₁), (p₂, q₂), ..., (p_n, q_n), .... wewnątrz niego. Oczywiście nie przypadkowy. Najpierw dbamy o to, by długość każdego odcinka była równa 1/3ⁿ. Czyli pierwszy odcinek ma długość 1/3, drugi 1/9, trzeci 1/27 etc. Poza tym każdy kolejny zawierać winien się w poprzednim. I wreszcie: przy każdym kroku dbamy o to, aby w n-tym odcinku nie było n-tego wyrazu zadanego nam ciągu rzeczywistego.

Konkretnie może to wyglądać następująco:

1)                 Dzielimy odcinek (0, 1) na trzy części – od zera do 1/3, od 1/3 do 2/3, wreszcie od 2/3 do 1. Czyli mamy (0, 1/3], (1/3, 2/3), [2/3, 1). Sprawdzamy, ile wynosi a₁. Przypuśćmy (dla przykładu), że wyraz ten wynosi np. 3/4. Zatem na pewno nie mieści się w (1/3, 2/3). Nie mieści się też w (0, 1/3], ale załóżmy dla ustalenia uwagi, że bardziej podoba nam się (1/3, 2/3). Przyjmujemy, że w naszym ciągu odcinków p₁ to 1/3, q₁ to 2/3. Czyli (p₁, q₁) to (1/3, 2/3).

2)                 W kolejnym kroku dzielimy (1/3, 2/3) znów na trzy części: (1/3, 4/9), [4/9, 5/9), [5/9, 6/9). Sprawdzamy wyraz a₂ i wybieramy taki przedział, do którego a₂ nie należy. Być może okaże się to przedział środkowy i wtedy mamy (p₂, q₂) = (4/9, 5/9).

Analogicznie postępujemy w kolejnych krokach, rzecz jasna – nieskończenie wielu. Odcinki są coraz węższe i zbiegają (używamy tu tego słowa trochę nieformalnie, bo nie wprowadzaliśmy ściśle zbieżności) do pewnego punktu c. Punkt ten jest przy rosnących n granicą ciągu lewych krańców (p_n) i zarazem prawych krańców (q_n), tzn. Zbliżają się one do siebie.

Czy możliwe, by c był równy któremuś z wyrazów zadanego nam na początku ciągu a_n, który w każdym kroku staraliśmy się tak skrzętnie "wyminąć"? Nie, bo nasz ciąg odcinków konstruujemy tak, by a_n nie należał do p_n, q_n (gwarantujemy sobie, że jest tak dla każdego n), natomiast c należy do każdego z naszych odcinków (jako ich przekrój, a więc z definicji, przekrój pewnej rodziny zbiorów to bowiem te elementy, które należą do każdego z nich). A zatem c jest obiecaną na początku wywodu liczbą rzeczywistą, której na pewno nie ma w ciągu a_n – który był ciągiem dowolnym, co czyni nasze rozumowanie ogólnym.

To nie wszystko. Przytoczymy jeszcze dowód przedstawiony m.in. w książce Couranta i Robbinsa "Co to jest matematyka?", choć nie jest on do końca precyzyjny, ale poglądowo bardzo ciekawy. Znów posłużymy się tylko odcinkiem (0, 1). Załóżmy, że zbiór wszystkich punktów z tego odcinka da się ułożyć w ciąg a₁, a₂, a₃ ... Stwórzmy wokół pierwszego elementu ciągu, tj. punktu a₁, przedział długości 1/10. Wokół a₂ tworzymy kolejny przedział – długości 1/100 (podnosimy 10 do kwadratu). Wyraz trzeci zamykamy w przedziale długości 1/1000. Tradycyjnie możemy rzec: i tak dalej. Co z tego wynika? Jeśli rzeczywiście wszystkie punkty odcinka należą do ciągu, to cały ten odcinek jest pokryty przez zachodzące na siebie przedziały, ściślej: przez nieskończony ciąg coraz mniejszych przedziałów. Na przykład może być tak, że tysięczny wyraz wynosi 0,9 – i wokół 0,9 tworzymy malutki przedział długości 1/10¹⁰⁰⁰. Wspaniale, ale co z tego?

Otóż możemy zmierzyć sumę długości tych przedziałów. Po co, zapyta ktoś? Skoro pokrywają cały przedział (0, 1), a pokrywają, bo tworzone są wokół każdego punktu, to suma ich długości wynosi z pewnością co najmniej 1 (co najmniej, bo mogą na siebie zachodzić i będziemy mieć "nadmiarowe" długości).

Okazuje się, że nie. Pierwszy przedział ma długość 1/10, drugi 1/10², trzeci 1/10³ itd. Cóż to jest? Ciąg (postęp) geometryczny, którego granica to 1/9. Mnożymy bowiem – według znanego wzoru – pierwszy wyraz (1/10) przez wyrażenie 1/(1-q), gdzie q to także 1/10. Czyli 1/10 mnożymy przez 10/9 i otrzymujemy 1/9. Wygląda na to, że cały przedział (0, 1) można pokryć ciągiem przedziałów, których suma długości jest niewątpliwie dużo niższa niż 1, choć podobno "zajmują" cały przedział. Po raz kolejny założenie o przeliczalności liczb rzeczywistych, tj. o możliwości ułożenia ich w ciąg, a co za tym idzie – o możliwości ułożenia liczb z (0, 1) w ciąg – doprowadziło nas do sprzeczności.

W drugiej części dowiemy się, dlaczego liczb w dwuwymiarowym kwadracie jest tyle samo, co na jednowymiarowym odcinku (a zatem - dlaczego płaszczyzna i prosta są równej mocy), pokażemy również, że zbiór wszystkich podzbiorów danego zbioru A ma większą moc niż A.