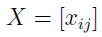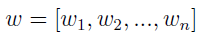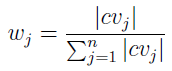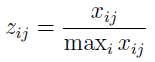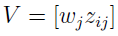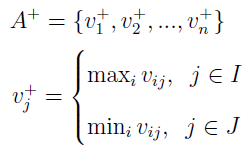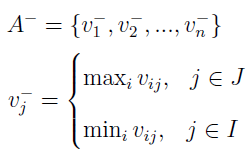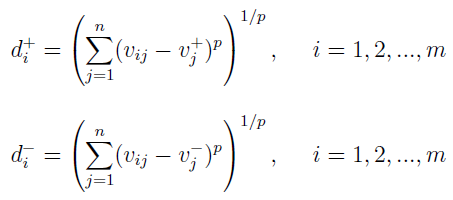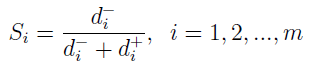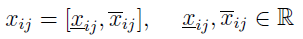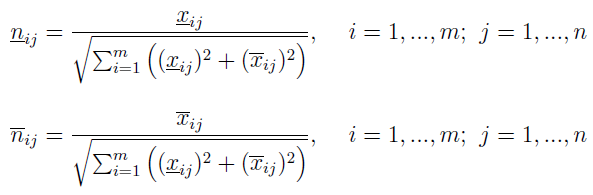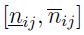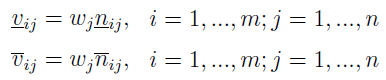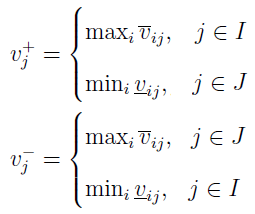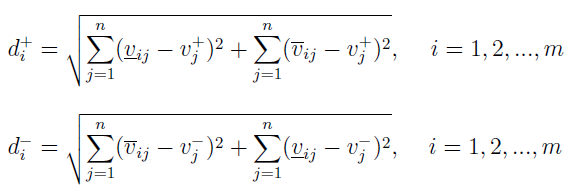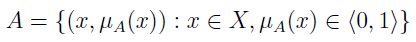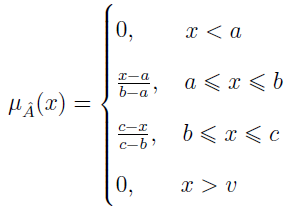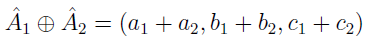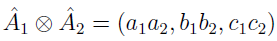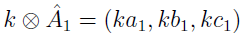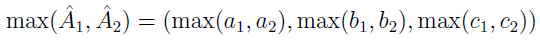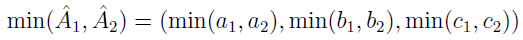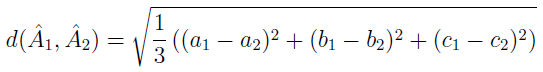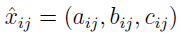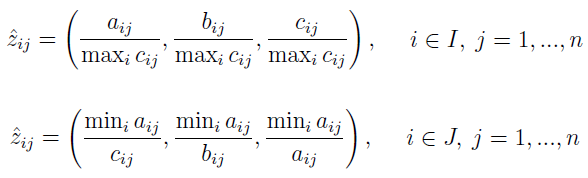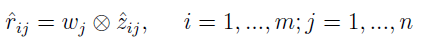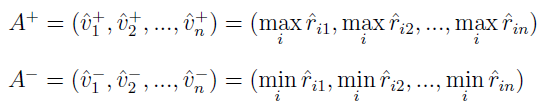Metoda TOPSIS w analizie wielokryterialnej

Algorytm TOPSIS to jedna z wygodniejszych i bardziej znanych metod rozstrzygania problemów wielokryterialnych. Tego rodzaju zagadnienia spotkać można w wielu dziedzinach życia, w szczególności w szeroko pojętym planowaniu finansowym i gospodarczym.

Przykłady można sobie łatwo wyobrazić. W logistyce może chodzić o określenie najlepszej trasy dla ciężarówki czy statku. W handlu i produkcji - o wybór najlepszego dostawcy towarów czy surowców. W grze na giełdzie i forexie - o skonstruowanie najefektywniejszego portfela inwestycyjnego. W informatyce - o rozpoznanie najlepszego modelu sieci komputerowej.

Najlepszy. Co właściwie znaczy to słowo? Czy tyle co najtańszy? Najszybszy? Najbezpieczniejszy? Rzecz w tym, że interesują nas wszystkie te kryteria. Chcielibyśmy możliwie tanio, możliwie szybko, możliwie bezpiecznie, możliwie bezawaryjnie itd. Nie ma problemu, gdy scenariuszy jest tylko kilka i któryś z nich wyróżnia się w oczywisty sposób, bo daje najbardziej obiecujące wyniki według każdego kryterium. Ale często tak nie jest. Mamy bardzo wiele scenariuszy, sporo cech, na które patrzymy - a dodatkowo tam, gdzie jest najtaniej, tam nie jest najszybciej. I na odwrót. Przypomina to naciąganie zbyt małego prześcieradła na łóżko. Trudno znaleźć rozwiązanie nie tylko w mgnieniu oka, ale nawet po długich dociekaniach - o ile bazujemy tylko na swoich przeczuciach albo rachunkach prowadzonych bez konkretnej metodologii.

W innym tekście edukacyjnym opisywaliśmy metodę TMAI - Taksonomiczną Miarę Atrakcyjności Inwestowania. W dużym skrócie jej idea jest taka: każdej z badanych spółek przypisujemy wektor, którego elementami są wskaźniki znane z analizy wskaźnikowej (np. płynność bieżąca, ogólne zadłużenie etc.). Z całej puli wybieramy najlepsze wartości (zwykle najwyższe, choć oczywiście zadłużenie powinno być jak najmniejsze) - np. płynność ze spółki A, wypłacalność natychmiastową ze spółki C, zwrot z kapitału własnego ze spółki F itd. Tak powstaje wektor wzorcowy - spółka teoretyczna, idealna. Następnie przy pomocy pewnych narzędzi matematycznych mierzymy 'odległość' pozostałych spółek od tego ideału. Te, które są najbliżej, są najlepsze.

TOPSIS opiera się na podobnym rozumowaniu, choć jest to metoda o szerszych, jak się wydaje, zastosowaniach. Ma także różne warianty: przedziałowy, rozmyty i inne.

TOPSIS to skrót od Technique for Order of Preference by Similarity to Ideal Solution. Algorytm ten w roku 1981 zaprezentowali Hwang i Yoon, aczkolwiek - jak podają E. Roszkowska i T. Wachowicz - znacznie wcześniej podobne podejście propagował polski statystyk Z. Hellwig.

Przejdźmy do rzeczy. Będzie trochę wzorów matematycznych, ale czytelnik łatwo się przekona, że nie są one aż tak skomplikowane, jak się wydają. Bazujemy głównie na pracy E. Roszkowskiej i T. Wachowicza (por. bibliografia), czerpiąc z niej główny tok wywodu i wzory; w tle jednak przewijają się także inne źródła.


Model podstawowy

Zaczniemy od klasycznej wersji TOPSIS. Problem decyzyjny jest tu dyskretny. Oznacza to, że przynajmniej część zmiennych decyzyjnych przyjmuje wartości dyskretne, tj. ze zbioru równolicznego z liczbami naturalnymi. A więc np. naturalne, całkowite czy wymierne. Dane wejściowe są określone dokładnie przy pomocy liczb - mamy np. dostawcę nr 1, który jest odległy o 20 km i żąda 30.000 zł; oraz dostawcę nr 2, którego magazyny są położone 100 km od nas, ale za to żąda on tylko 26.000 zł. I tak dalej.

A zatem mamy m wariantów czy też scenariuszy oraz n kryteriów. Realizację j-tego kryterium w i-tym wariancie (czyli np. cenę towaru u dostawcy nr 2 albo odległość dostawcy nr 3) zapisujemy jako x_ij. W ten sposób powstaje macierz danych:

Druga rzecz to wektor wag. Nie wszystkie kryteria muszą być dla nas tak samo ważne. Może się zdarzyć, że choć chcielibyśmy kupić towary tanio, to jednak jeszcze bardziej zależy nam na czasie (lub odwrotnie). Stąd ów wektor:

Wagi te powinny sumować się do 1. Inną kwestią jest to, skąd je wziąć. Cóż, w to zagadnienie nie będziemy się zagłębiać. Można ustalić równe wagi dla wszystkich kryteriów. Można dobrać je na wyczucie albo na podstawie ankiety przeprowadzonej wśród ekspertów (wtedy zapewne będziemy bazować na ich intuicji...). Istnieją także metody formalne. Na przykład:

Otóż przez cv_j rozumiemy współczynnik zmienności (coefficient of variation) poziomu realizacji wariantów dla j-tego kryterium.

Dodajmy jeszcze, że nasze kryteria dzielimy na dwa zbiory: I (tam trafiają te, które maksymalizujemy, np. zysk) i J (to cechy, które chcemy zminimalizować, np. opłata czy zanieczyszczenie).

Wróćmy do głównego wątku. Otóż różne kryteria mogą być mierzone według odmiennych skal, a przecież my chcemy rozmawiać po prostu o liczbach. Jeśli jednak mamy 120 KM (koni mechanicznych) i 145.000 zł (jako cenę samochodu), to otrzymujemy liczby 120 i 145.000. Trudno je ze sobą zestawiać. Stąd też stosuje się procedurę normalizacji, a więc sprowadza się wielkości do rzędu porównywalności. Można to zrobić na wiele sposobów, np. E. Roszkowska i T. Wachowicz wymieniają trzy; my prezentujemy tylko jeden z nich:

Przez max_i x_ij rozumiemy maksymalną wartość poziomu realizacji j-tego kryteriów wyznaczoną po wszystkich wariantach decyzyjnych.

Normalizację stosowaliśmy także przy metodzie TMAI. Tam, aby uzyskać z_ij, odejmujemy od wyjściowej wartości średnią arytmetyczną zmiennej (np. średnią z wyników badanych spółek za dany rok) i dzieliliśmy przez odchylenie standardowe tejże zmiennej (cechy). Ale to dygresja.

Teraz mnożymy wartości dla każdego kryterium przez odpowiednią dlań wagę i w ten sposób otrzymujemy znormalizowaną macierz decyzyjną, która wykorzystuje wprowadzone wcześniej wagi:

Kolejny krok to znalezienie dwóch specjalnych wektorów. Jeden z nich jest wzorcem (ponownie kłania się TMAI) i nazywa się go z angielska PIS (Positive Ideal Solution). Drugi jest anty-wzorcem, to NIS (Negative Ideal Solution). A zatem ideał i kontr-ideał.

Wyglądają one, w tej właśnie kolejności, następująco:

Ideał, jak łatwo zauważyć, zawiera najwyższe wartości zmiennych maksymalizowanych i najniższe minimalizowanych. Ściślej: ustalamy j (kryterium) i idziemy po wszystkich wariantach. Wybieramy maksimum (np. największy zysk), jeśli j należy do I. A jeżeli należy do J, to wybieramy minimum (np. najniższy koszt). Kontr-ideał jest skonstruowany odwrotnie.

Teraz obliczamy odległość rozpatrywanych wariantów od wzorca (ideału) i anty-wzorca. Można tu stosować rozmaite metryki, my prezentujemy wzory wykorzystujące tzw. odległość Minkowskiego. Inną opcją jest odległość Mahalanobisa, o której pobieżnie wspominaliśmy przy opisie TMAI (bo i tam można ją stosować).

A zatem przed nami wzory według metryki Minkowskiego:

Odległości są indeksowane literką i przyjmującą wartości od 1 do m. A zatem dotyczą one wariantów (np. pierwszej, drugiej i trzeciej trasy). Zakładamy, że p jest większe od lub równe 1. Przy p = 2 otrzymujemy standardową odległość euklidesową.

Ostatnia rzecz to finalny miernik, który wygląda tak:

Jak widać, odległość od anty-wzorca dzielimy przez sumę obu odległości. S przyjmuje wartości od 0 do 1. Im wyższe - tym lepsze.


Przypadek przedziałowy

Rozważa się sytuację, w której elementy macierzy decyzyjnej to nie konkretne liczby, ale przedziały liczbowe. Na przykład wiemy, że czas podróży trasą nr 1 to od 120 do 125 minut, na trasie nr 2 oszacowanie to od 95 do 110 minut. Albo: dostawca nr 1 zapowiada, że urządzenie, które chce nam sprzedać, będzie pracować bez awarii co najmniej 24 miesiące, ale nie więcej niż 30 miesięcy, zarazem produkując od 90 do 100 kg cukru dziennie, w zależności od jakości surowca. Drugi doradca podaje inne przedziały dla swojej maszyny, trzeci jeszcze inne.

A zatem teraz elementy naszej macierzy wyglądają tak:

Według Jahanshahloo, Hosseinzadeha Lofti i Izadikhaha można je znormalizować przy pomocy następujących wzorów:

A zatem to, co widzimy poniżej, jest znormalizowanym przedziałem:

Stosujemy wcześniej przedstawione podejście: macierz znormalizowaną, która uwzględnia wagi. Jej wyrazy to przedziały, których dolne i górne granice określone są tak:

Następny ruch to wyznaczenie wektorów idealnego i kontr-idealnego. Oznaczenia są takie jak wcześniej, postaci wektorów też, natomiast ich wyrazy podane są tymi wzorami:

W skrócie można powiedzieć, że teraz interesują nas najwyższe i najniższe granice znormalizowanych przedziałów. Odległości wariantów od obu specjalnych wektorów są obliczane podobnie jak wcześniej:

Wzór ostatecznego miernika S również pozostaje bez zmian.


Model rozmyty

Model rozmyty odwołuje się do pojęcia zbiorów rozmytych (fuzzy sets), które zostało wprowadzone do matematyki przez L. A. Zadeha. Na bazie tego terminu powstała gałąź logiki matematycznej, tzw. logika rozmyta (fuzzy logic). Należy ona do szerokiej puli logik nieklasycznych (inne to np. logiki modalne, intuicjonizm i systemy superintuicjonistyczne, logiki wielowartościowe czy parakonsystentne). W rzeczywistości można jednak mówić o zbiorach rozmytych bez uruchamiania nowoczesnej aparatury logicznej.

Idea zbioru rozmytego jest zresztą bardzo naturalna. Odwołuje się do typowego w codziennym życiu problemu: do faktu, że pewne rzeczy są jakieś, ale tylko "trochę", "poniekąd", "częściowo", "do pewnego stopnia". A zatem chodzi o terminy nieostre, przybliżone.

W ogólności zakładamy, że mamy jakiś zbiór X (przestrzeń obiektów) i na jego podstawie konstruujemy zbiór rozmyty A:

Jak łatwo zauważyć, elementami A są pary uporządkowane; pierwszym ich elementem jest jakiś obiekt z X, a drugim funkcja przynależności μ_A. Funkcja ta każdemu obiektowi z X przypisuje wartość z przedziału domkniętego od 0 do 1. Jeśli μ_A(x) = 0, to mówimy, że x z całą pewnością nie należy do A. Jeżeli μ_A(x) = 1 - to x na pewno jest w A. A jeśli wartość funkcji mieści się gdzieś pomiędzy tymi skrajnościami, to x "częściowo" należy do A.

Istnieją różne zbiory rozmyte, nas będą interesować tzw. trójkątne liczby rozmyte. Są to trójki uporządkowane postaci (a, b, c), których funkcja przynależności wygląda jak poniżej:

Załóżmy np., że a = 7.5, b = 8.0, c = 8.5. Powiedzmy, że jest to liczba "około 8". Jeśli x = 8.2, to funkcja przynależności przyjmuje wartość 0.3 / 1 = 0.3. A zatem, zgodnie z intuicją 8.2 "częściowo" należy do liczby rozmytej "około 8".

Jeżeli funkcja przynależności jest równa 0 dla x nie większych niż 0, to liczba jest "dodatnia". Takie dodatnie liczby rozmyte (a1, b1, c1) i (a2, b2, c2) można:

- dodawać:

- mnożyć:

- mnożyć przez skalar:

- znajdować ich maksima:

- oraz minima:

- a także mierzyć odległości między nimi (nie mylić z odległością w TOPSIS):

Właśnie, TOPSIS. Wracamy na główny tor. Tym razem nasza macierz decyzyjna składa się z liczb rozmytych. Na przykład pierwszy kierowca przejedzie trasę w ciągu ok. 2 godzin, zużywając ok. 7 litrów paliwa, drugi potrzebuje tylko ok. 1,5 godziny - i mniej więcej 6 litrów benzyny. Cena pierwszej akcji powinna za miesiąc wynosić ok. 25 zł, cena drugiej - ok. 17 zł. I tak dalej.

A zatem teraz każdy element macierzy ma taką postać:

Mamy zatem trzy wartości: a_ij - pesymistyczną, b_ij - najbardziej prawdopodobną, c_ij - optymistyczną.

Normalizację wykonuje się takimi wzorami:

Tak natomiast powstają elementy macierzy decyzyjnej V z wagami:

Wektory wzorcowe (ten "dobry" i ten "zły") mają taką postać:

A tak liczy się odległość wariantu do wzorca i anty-wzorca. Co znamienne, korzystamy tu już nie z metryki Minkowskiego, tylko z przedstawionego wcześniej wzoru na odległość między dwiema liczbami rozmytymi.

Istnieją jeszcze inne rozszerzenia i ulepszenia metody TOPSIS, temat jest cały czas badany przez informatyków, ekonometrów i matematyków. Algorytm jest również dostępny w programach komputerowych i dodatkach do arkuszy kalkulacyjnych czy pakietów statystycznych.

Adam Witczak


BIBLIOGRAFIA:

E. Roszkowska, T. Wachowicz, "Metoda TOPSIS i jej rozszerzenia - studium metodologiczne", w: "Analiza wielokryterialna. Wybrane zagadnienia", seria "Informatyka w badaniach operacyjnych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013.

"Zastosowanie logiki rozmytej w ekonomii - wybrane modele decyzyjne", w: "Metody i modele analiz ilościowych w ekonomii i zarządzaniu", Wydawnictwo Akademii Ekonomicznej w Katowicach 2009.

A. Tikhonenko, "Przedziałowe rozszerzenie metody TOPSIS", Studia i Materiały, EWSIE w Warszawie, nr 1(5) 2013.

Chang, Lin, Chiang, Ho, "Domestic Open-End Equity Mutual Fund Performance Evaluation Using Extended TOPSIS Method with Different Distance Approaches", Expert Systems with Applications, vol. 37, issue 6, June 2010.

K. Rudnik, D. Kacprzak, "Rozmyta metoda TOPSIS wykorzystująca skierowane liczby rozmyte", Konferencja Innowacje w Zarządzaniu i Inżynierii Produkcji 2015.

Z. Piotrowski, "Algorytm doboru metod wielokryterialnych w środowisku niedoprecyzowania informacji preferencyjnej", Zachodniopomorski Uniwersytet Technologiczny, Szczecin 2009.