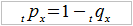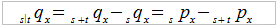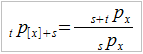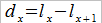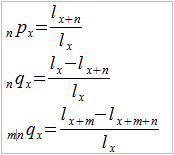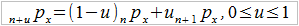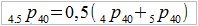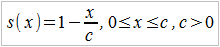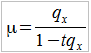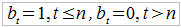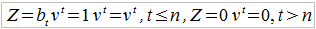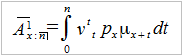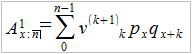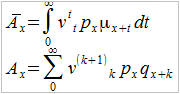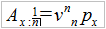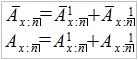Ubezpieczenia na życie - podstawy

Ubezpieczenia na życie, o czym wspominaliśmy już w naszym poprzednim tekście o tematyce aktuarialnej, zaliczają się do tzw. Działu I w towarzystwach ubezpieczeniowych. Formalnie – według ustawy – obejmuje on polisy: 1) na życie, 2) posagowe, zaopatrzenia dzieci, 3) na życie, związane z funduszem inwestycyjnym, 4) rentowe, 5) wypadkowe i chorobowe – ale jako uzupełnienie grup 1) – 4).

W niniejszym materiale poznamy najbardziej podstawowe wzory i pojęcia z tematyki ubezpieczeń typu life. Będą to wiadomości o charakterze teoretycznym i matematycznym, co nie powinno odstraszać czytelnika (a wręcz przeciwnie), jako że te wzory i terminy są niezbędne choćby na każdym kursie (wykładzie uczelnianym) z omawianej tematyki. Zaznaczmy jednak, że w opracowaniu tym nie będziemy zbyt szczegółowo wchodzić w probabilistyczne podstawy teorii, ani tym bardziej – w dowody.

Spójrzmy na jeden z najbardziej znanych wzorów, zawierający zresztą w sobie dwa nader istotne symbole:

Lewa strona wzoru oznacza prawdopodobieństwo tego, że x-latek przeżyje więcej niż czas t. Na przykład, że 40-latek przeżyje co najmniej 5 lat. Widzimy, patrząc na stronę prawą, że jest to dopełnienie innego prawdopodobieństwa, mianowicie _tq_x, tj. takiego, że x-latek umrze przed upływem czasu t. A więc, że nasz przykładowy 40-latek umrze zanim minie 5 lat. Intuicyjnie jest to dość oczywiste równanie: jeśli x-latek ma przeżyć przynajmniej t lat (być może dużo więcej), to musimy "pozbyć się" opcji, w której nie dożywa x+t lat.

Tak naprawdę czas nie musi tu oznaczać jedynie kolejnych lat, można mówić też o większej dokładności (np. 3 lata i 23 dni), a w rozważaniach teoretycznych pojmuje się wręcz ów czas jako ciągły, przebiegający wszystkie liczby rzeczywiste (w każdym razie wszystkie dodatnie).

Drugi ważny wzór określa nam prawdopodobieństwo tego, że nasz x-latek przeżyje jeszcze s lat, ale później umrze w czasie t:

Voila. Widzimy tu dwie równoważne interpretacje tego scenariusza. W pierwszej bierzemy najpierw, by posłużyć się wartościami przykładowymi, prawdopodobieństwo tego, że obecny 40-latek umrze przed upływem np. 15 lat (s=10, t=5) – i odejmujemy możliwość, że umrze już przed upływem 10 lat. A więc 10 lat musi przeżyć, natomiast później najwyżej 5. W drugiej wersji myślimy analogicznie, ale biorąc pod uwagę przeżycie więcej niż s lub s+t lat.

I jeszcze jedno pojęcie – prawdopodobieństwo warunkowe, że x-latek przeżyje kolejne t lat, o ile najpierw przeżyje przynajmniej s lat:

Pomijamy tu rozważania nad tym, dlaczego mamy [x], a nie po prostu x. Okazuje się zresztą, że przy założeniu tzw. hipotezy jednorodnej populacji, co nader często robi się w rozważaniach teoretycznych, spokojnie można nawiasy kwadratowe pominąć.

Cztery wprowadzone w poprzednich akapitach symbole obowiązkowo trzeba znać. Warto też wiedzieć, czym są tablice trwania życia – aczkolwiek już sama ich nazwa pozwala domyślić się, o co chodzi. Są to tablice, które na bazie empirycznych badań pokazują nam, ile osób (osobno kobiet i mężczyzn) w danej zbiorowości (de facto mówimy tu o Polakach, a zarazem o populacji liczącej 100 tys. osób) dożywa określonego wieku x, a ile w tym wieku umiera. Pierwszą wielkość oznacza się jako l_x, drugą jako d_x. Oczywiste jest więc równanie:

Możemy zobaczyć, jak te wielkości mają się do poprzednich symboli (znów – zależności są dość intuicyjne):

To, że stosujemy tu literkę n, a nie t, wyraża po prostu fakt, że mamy na myśli liczby naturalne (lata), a nie czas ciągły. To może sprawiać wrażenie, że tablice trwania życia są mało przydatne, bo cóż począć, jeśli zechcemy wziąć pod uwagę to, że zgon człowieka nie musi następować na początku roku, ale w dowolnym momencie – np. 13 czerwca, czy wręcz w szczególności 13 czerwca, o godzinie 20:30:15.

Kwestię rozwiązują tzw. hipotezy interpolacyjne. Zazwyczaj rozpatruje się hipotezy: jednostajności (HU), przedziałami stałego natężenia zgonów (HCFM) oraz Balducciego (HB). My opiszemy tutaj tylko pierwszą z nich. Wyraża się ona wzorem:

Jak to rozumieć? Załóżmy, że chcemy obliczyć prawdopodobieństwo tego, że obecny 40-latek przeżyje więcej niż 4,5 roku. Otóż okazuje się (por. powyższy wzór), że potrzeba nam do tego wiedzy o tym, iż osobnik ten przeżyje co najmniej 4 lata – i tego, że co najmniej 5:

Mamy już więc wyjaśnioną wstępnie kwestię ułamkowego czasu życia. Warto jeszcze dodać, że tablice trwania życia nie są jedynym źródłem wiedzy o rozkładzie czasu trwania życia. Otóż czasami rozważa się też czysto teoretyczne, analityczne funkcje: przede wszystkim de Moivre'a, Gompertza, Makehama i Weibulla. Najprostszy jest wzór de Moivre'a. Zakłada on, że:

Wyjaśnijmy, że c (czasami oznaczeniem jest mała grecka omega) to pewna stała, maksymalny rozważany wiek (de Moivre zakładał tu 100 lat, współcześnie mogłaby to być większa liczba, jako że stulatków mamy całkiem sporo), natomiast s(x) to funkcja, która określa prawdopodobieństwo tego, że noworodek przeżyje przynajmniej x lat. A więc wzór ten sugeruje nam, że np. s(90) = 1 – 90/100 = 1/10. Czyli że prawdopodobieństwo, iż noworodek dożyje 90-tki jest 10-procentowe.

Można jeszcze wprowadzić tzw. intensywność wymierania, tj. prawdopodobieństwo zgonu w wieku dokładnie x lat. Oznacza się ją przez grecką literę μ. Przy hipotezie HU mamy:

Jeśli przed q_x lub p_x nie ma w dolnym indeksie liczby, to domyślnie jest to ₁qx oraz ₁px. Dodajmy, uprzedzając zarzut o błąd literowy, że przy HU mamy: _tqx = tqx. W przykładach książkowych często przyjmuje się jednak koncepcję stałej intensywności zgonów (wyrażonej zatem liczbą, np. 0,04).

Przejdźmy wreszcie do clou naszych wywodów. Przedstawimy najważniejsze wzory na jednorazowe składki netto. Taką składkę rozumie się jako wartość oczekiwaną zmiennej losowej opisującej wartość przyszłego świadczenia, jakie uzyska osoba ubezpieczona.

A więc mamy tu niejako do czynienia z dwiema operacjami: dyskontowania i uśredniania. Chodzi o to, że - wcielając się w rolę klienta - dajemy ubezpieczycielowi pewną kwotę (tak naprawdę często odbywa się to okresowo, np. co miesiąc, ale rozpatrujemy uproszczony model, w którym robimy to "raz, a dobrze"). Tenże ubezpieczyciel może ową kwotę inwestować przez kolejne lata, zakładamy, że przy określonej stopie procentowej, ozn. i. Ubezpieczyciel chce wiedzieć, ile musi zainwestować (a więc, ile wziąć od klienta), by w określonym momencie móc wypłacić (np. krewnym klienta) żądane świadczenie (odszkodowanie, sumę ubezpieczenia). Moment ten jest jednak losowy – być może klient zapłaci składkę i umrze zaraz potem (można się domyślać, że wtedy jego pieniędzmi obracano krótko, a tymczasem trzeba już wypłacać sumę odszkodowania), być może przeżyje jeszcze 20 czy 40 lat. Stąd też za składkę netto zasadniczo uważa się E(Z), gdzie Z to zmienna losowa określająca obecną wartość wypłaty, zależna w naturalny sposób od przyszłego czasu życia ubezpieczonej osoby.

Ubezpieczyciel ma nadzieję na powiększenie pozyskanej kwoty dzięki stopie procentowej (tak, by w końcu spłacić nas - i mieć jeszcze zarobek). Dzięki temu sens ma nawet ubezpieczenie na całe życie, o którym wspomnimy nieco niżej - mimo tego, że wszyscy nim objęci zgłoszą się (tzn. ich spadkobiercy) po wypłatę, ponieważ każdy z nas prędzej czy później umrze.

Niech v to czynnik dyskonta, tj. 1/(1+i), i to oczywiście stopa procentowa. Przez b_t oznaczamy kwotę przyszłego świadczenia w zależności od czasu. Zakładamy przy tym uproszczony wariant: albo ubezpieczony dostaje 0, albo 1.

Spójrzmy na przypadek terminowego ubezpieczenia na wypadek śmierci, przyjmujemy czas ciągły. Sens takiej umowy jest następujący: umawiamy się z firmą ubezpieczeniową, że jeśli umrzemy w ciągu n lat, to zakład wypłaci (np. naszym spadkobiercom) sumę 1 zaraz po naszej śmierci. Później umowa przestaje obowiązywać, nasza składka w takim scenariuszu byłaby więc w pewnym sensie "zmarnowana". Innymi słowy:

Jakie będzie nasze Z – czyli, przypomnijmy, obecna wartość świadczenia (zdyskontowana)? Otóż mamy:

Składkę wylicza się z ogólnego wzoru na wartość oczekiwaną ciągłej zmiennej losowej, my jednak nie będziemy w tym momencie wchodzić w uzasadnienia i dowody, podamy wzór:

W praktyce pożyteczniejszy może być wzór dyskretny, w którym całkę zastępuje szereg, interesują nas tylko pełne lata i zakładamy, że odszkodowanie (świadczenie) płacone jest na koniec roku, w którym klient zmarł. Wtedy mamy:

Do wyliczenia _kp_x czy q_x+k możemy wykorzystać np. tablice trwania życia. Reszta to już tylko sumowanie i mnożenie skończonej liczby wyrazów.

Powyższe ubezpieczenie ma pewną cechę, którą można postrzegać jako wadę. Otóż, by pozwolić sobie na odrobinę czarnego humoru, jeśli nie postaramy się o własną śmierć w okresie n lat, to nikt nic po nas nie dostanie. Stąd też rozpatruje się też ubezpieczenie na całe życie. W tym scenariuszu dostaniemy pieniądze po prostu po śmierci, niezależnie od tego, jak długo będziemy na nią czekać. Tutaj wzory to:

Jak widać, tu nieskończoności w całce nie ominiemy – niemniej będzie to w praktyce wymagało obliczenia całek niewłaściwych, a więc pewnych granic, co może być relatywnie proste. Gorzej, o dziwo, sprawa przedstawia się z nieskończonym szeregiem, tu używa się np. tzw. liczb komutacyjnych, w ten wątek nie będziemy jednak wchodzić.

Rozważmy jeszcze czyste ubezpieczenie na dożycie. W tej sytuacji świadczenie dostają nie ci, którzy umrą, ale przeciwnie – ci, którzy przeżyją okres ubezpieczenia. Tym razem więc zakładamy się nie tyle o to, że "uda" się nam umrzeć, ale – że uda się przeżyć.

Tutaj wzory okazują się banalne, przy czym n to czas obowiązywania umowy:

Jak widać, nie rozróżniamy tu kwestii ciągłości lub dyskretności. Innymi słowy, można pojmować n jako liczbę naturalną – lub jako dodatnią rzeczywistą. Formalnie, w modelu ciągłym należałoby nad A dać poziomą kreskę (to oczywiście tylko oznaczenie).

I wreszcie ubezpieczenie mieszane: na wypadek śmierci i dożycie, połączenie pierwszego z trzecim. Polega to na tym, że otrzymujemy wypłatę albo wtedy, gdy przeżywamy okres ubezpieczenia, albo – gdy umrzemy w określonym czasie.  Wzór to po prostu suma:

W niniejszym opracowaniu pomijamy dalsze warianty, które można rozpatrywać, a które wciąż zaliczyć można do podstawowych: jak ubezpieczenia odroczone o daną liczbę lat, albo też ubezpieczenia o rosnącej lub malejącej wielkości świadczenia. Zwracamy też uwagę na fakt, że wzięliśmy pod uwagę tylko koncepcję jednorazowej składki netto, podczas gdy w praktyce zakłady częściej stosują składki opłacane okresowo. Co więcej, mówimy ciągle o wersji netto, a nie brutto – a więc pomijamy kwestię określenia składki tak, by pozwalała pokryć np. koszty działania zakładu ubezpieczeniowego. Model nie bierze również pod uwagę konkurowania z innymi zakładami (o to, by składka w naszej ubezpieczalni była jak najniższa). Nie zmienia to jednak faktu, że na takich właśnie wzorach i założeniach bazuje każdy podstawowy kurs matematyki ubezpieczeń life.

Adam Witczak

Bibliografia:

P. Kowalczyk, E. Poprawa, W. Ronka-Chmielowiec, Metody aktuarialne, PWN 2013

B. Błaszczyszyn, T. Rolski, Podstawy matematyki ubezpieczeń na życie, WNT 2004