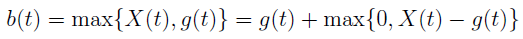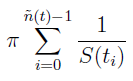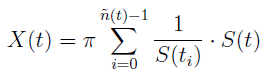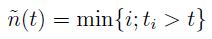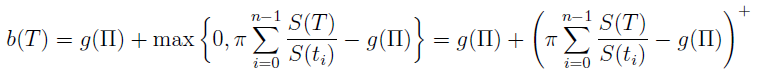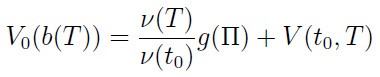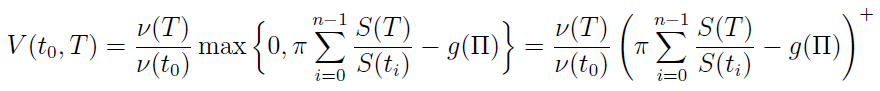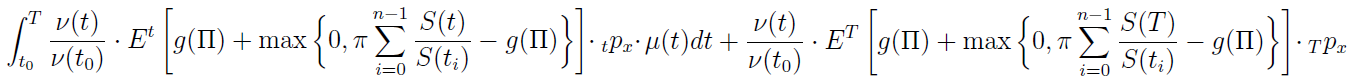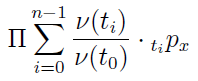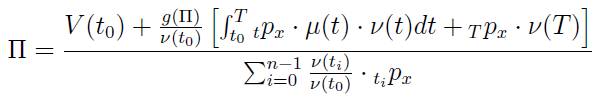Ubezpieczenia unit-linked

Ubezpieczenie typu unit-linked należy do gamy tych produktów ubezpieczeniowych, w których składka jest (przynajmniej częściowo) inwestowana na rynku kapitałowym. Inne możliwe rozwiązania tego typu to np. ubezpieczenia partycypacyjne czy equity-linked, o nich jednak nie będziemy mówić.

Idea polisy typu unit-linked jest następująca. Klient opłaca (jednorazowo lub okresowo) składkę, której część lokowana jest w portfelu funduszy inwestycyjnych. Fundusze te prowadzone są przez różne firmy - zewnętrzne w stosunku do towarzystwa ubezpieczeniowego. Towarzystwo dokonuje jednak cyklicznej (np. corocznej) weryfikacji portfela, co polega na wycofaniu z niego funduszy przynoszących słabe wyniki i wstawieniu w ich miejsce funduszy generujących przyzwoite zyski. Wypłata dla klienta lub jego spadkobierców następuje w określonym momencie, np. po zgonie tegoż klienta. Teoretycznie można sobie też wyobrazić wydarzenie innego typu, np. po prostu upływ określonej liczby miesięcy czy lat (ubezpieczenie terminowe).

Składka płacona przez ubezpieczającego się jest, jak zasygnalizowaliśmy wyżej, dzielona na dwie części. Jedna z nich ma charakter inwestycyjny, druga ochronny. Do tego za chwilę wrócimy.

Interesować będzie nas obliczenie tejże składki, tzn. dokonanie jej wyceny przy pomocy metod matematyki aktuarialnej. Bazować będziemy na pracy M. Homy (por. bibliografia), z której zaczerpnięto większość wzorów i oznaczeń.

Zacznijmy właśnie od oznaczeń. Będą one następujące:

Π - wysokość składki

π - część składki inwestowana w portfel

t_i - moment, w którym opłacana jest składka okresowa

X(t) - wartość portfela ubezpieczeniowego w chwili t

S(t) - cena jednostki aktywów w chwili t

g(t) - suma gwarantowana klientowi w momencie t

b(t) - świadczenie wypłacone klientowi w chwili t

_tp_x - prawdopodobieństwo tego, że x-latek przeżyje więcej niż czas t (jedno z typowych oznaczeń matematyki aktuarialnej).

W momencie zajścia zdarzenia losowego, którego dotyczy kontrakt, towarzystwo wypłaca klientowi większą z dwóch wartości. Pierwszą stanowi minimalna gwarantowana suma ubezpieczenia, drugą - wartość rynkowa portfela.

Można to zapisać poniższym wzorem:

Zauważmy, że cała konstrukcja jest podwójnie losowa. Losowy jest bowiem zarówno moment wypłaty (przynajmniej jeśli chodzi o zgon klienta), jak i wielkość świadczenia. Ten drugi fakt wynika z tego, że nie możemy być pewni tego, na ile będzie opiewał portfel. To przecież zależy od tego, ile zdążyliśmy weń zainwestować i jak powiodły się działania prowadzone na rynku przez fundusze.

Otóż w momencie t mamy w portfelu taką liczbę jednostek wybranych aktywów:

Tym samym wartość całego portfela w chwili t określona jest tak:

Zakładamy przy tym, że:

Na podstawie powyższych rozwiązań możemy wyznaczyć wypłatę w chwili wygaśnięcia ubezpieczenia:

Wyrażenie g(Π) może być w pierwszej chwili mylące, ponieważ wyżej definiowaliśmy g jako funkcję czasu (zmiennej t), tu natomiast mamy g zależne od wysokości składki. Należy więc g(Π) rozumieć jako sumę gwarantowaną przy danej składce Π, wpłaconej do momentu T.

Wartość rynkowa wypłaconego świadczenia jest w chwili t₀ równa tyle:

przy czym:

Otóż okazuje się, że V(t₀, T) to funkcja wypłaty europejskiej opcji kupna o terminie wygaśnięcia T z ceną wykonania, która równa jest sumie gwarantowanej g(Π).

Należy jeszcze przypomnieć, że ν(t) to czynnik dyskonta, tj. e^-δ, gdzie δ to tzw. intensywność oprocentowania.

Jak to już mówiliśmy na początku, składka dzieli się na dwie części. Jeśli przez Π rozumiemy składkę płaconą w chwili t_i, to π= k Π, k należy do [0, 1]. Oczywiście π to właśnie ta część składki, która jest inwestowana w fundusze.

Dalej, w ślad za pracą, na której bazujemy, będziemy analizować ubezpieczenie unit-linked o charakterze mieszanym. To znaczy, że towarzystwo wypłaca zarówno kwotę z tytułu dożycia do końca okresu, jak i sumę, która jest należna w momencie zajścia zdarzenia objętego kontraktem (np. zgonu).

Do wyliczenia składki stosuje się następującą zasadę. Otóż wartość oczekiwana zaktualizowanych wpływów z tytułu składek powinna być równa wartości oczekiwanej zaktualizowanych przepływów związanych z wypłacanymi świadczeniami. Wygląda to - w ogólności - tak:

Otóż prawą stronę - według wzorów matematyki aktuarialnej, uwzględniających całki - rozpisujemy następująco:

Trzeba przyznać, że wzór ten robi wrażenie swoją złożonością, acz jeśli czytelnik wróci do wzoru nr 6, to sprawa stanie się bardziej zrozumiała (polecamy też np. nasz artykuł na temat podstaw matematyki ubezpieczeń na życie). To, że wzór jest sumą dwóch składników, wynika z faktu, że ubezpieczenie, jak już pisaliśmy, ma charakter mieszany. Czyli: otrzymujemy wypłatę albo wtedy, gdy przeżywamy okres ubezpieczenia, albo – gdy umrzemy w określonym czasie. Fakt, że może zdarzyć się jedno lub drugie, jest uwzględniony przy pomocy prawdopodobieństw. Przez μ(t) rozumiemy tzw. natężenie zgonów (odsyłamy tutaj do podręczników aktuarialnych, por. bibliografia).

Ale to jeszcze nie jest wzór na składkę. Należy w nim uwzględnić także zdyskontowaną wartość składek:

Zaprezentowane wyżej wartości podstawia się do ogólnego wzoru jako lewą i prawą stronę, wykonuje się proste przekształcenia matematyczne i tym sposobem dochodzi się do następującego rezultatu:

M. Homa w swoim opracowaniu analizuje także przykładowe ubezpieczenia typu unit-linked, rozważając różne sposoby kapitalizacji oraz tablice umieralności oparte na prawie Makehama. Wnioskiem jest m.in. stwierdzenie, że składka netto w takim ubezpieczeniu to rosnąca wypukła funkcja udziału inwestycyjnej części składki. Poza tym wyższy procent inwestowanej części składki zwiększa ryzyko ubezpieczonego. Towarzystwo ubezpieczeniowe minimalizuje dzięki ubezpieczeniom unit-linked swoją funkcję ochronną, cedując ryzyko finansowe na klienta.

Adam Witczak

BIBLIOGRAFIA:

M. Homa, "Kalkulacja składki w inwestycyjnych ubezpieczeniach na życie typu unit-linked", w: "Ubezpieczenia wobec wyzwań XXI wieku", red. W. Ronka-Chmielowiec, Wydawnictwo Uniwersytetu Ekonomicznego we Wrocławiu 2011

P. Kowalczyk, E. Poprawa, W. Ronka-Chmielowiec, Metody aktuarialne, PWN 2013

B. Błaszczyszyn, T. Rolski, Podstawy matematyki ubezpieczeń na życie, WNT 2004