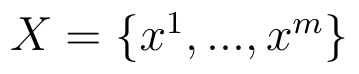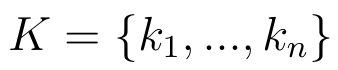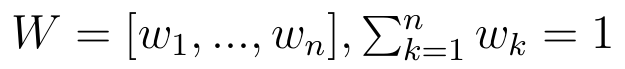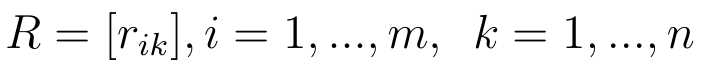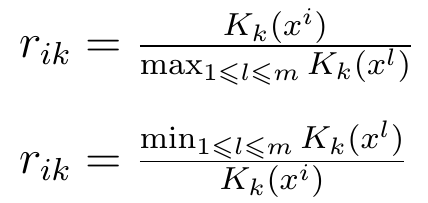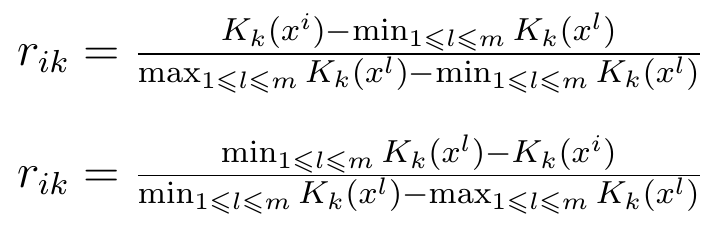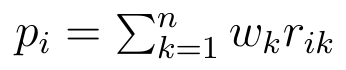SAW - metoda średniej ważonej

Metoda sumy ważonej to jeden z najbardziej znanych algorytmów analizy wielokryterialnej. Jest on zresztą dość prosty, szczególnie w swoim podstawowym wariancie.

SAW (Simple Additive Weighting) przedstawiona została po raz pierwszy w roku 1954, mianowicie w pracy C. W. Churchmana i R. L. Ackoffa "An Approximate Measure of Value", opublikowanej w "Journal of Operations Research Society of America".

Główna idea jest prosta. Po pierwsze, mamy (jak zwykle w zagadnieniach MCDM - Multi-Criteria Decision Making) zbiór wariantów decyzyjnych, czyli pewnych scenariuszy, które chcemy ostatecznie uszeregować od najlepszego do najgorszego (lub odwrotnie). Jest ich m, więc zbiór zapisać można tak:

Taki scenariusz to np. spółka, której akcje chcemy kupić; nieruchomość, którą chcemy nabyć; firma, z którą chcemy rozpocząć współpracę itd.

Po drugie: spółkę, firmę, nieruchomość czy państwo oceniać możemy według wielu różnych kryteriów. Zazwyczaj potencjał naszej oceny "na oko" wyczerpuje się dość szybko i zaczynamy się gubić: spółka A ma najlepszą płynność bieżącą, ale spółka B wiedzie prym pod względem rentowności netto. Każda z nich jest jednak według pewnego kryterium najgorsza, podczas gdy np. spółka C nigdy nie zajmuje ani ostatniego, ani pierwszego miejsca. Do tego dochodzą kolejne podmioty: D, E, F... Może być ich dużo. I kolejne kryteria. Na przykład na naszym portalu zwykle badamy firmy z GPW pod kątem rentowności na poziomach EBITDA, operacyjnym i netto (czasem też brutto na sprzedaży), złotej reguły bilansowej, poziomu zadłużenia, płynności bieżącej, wypłacalności natychmiastowej oraz zwrotów ROE i ROA. Niekiedy dochodzi do tego również rotacja aktywów.

Tak więc mamy n kryteriów (oczywiście n nie ma żadnego związku z m, choć w szczególności mogą być one równe):

Niekoniecznie musi być tak, że każde kryterium jest jednakowo ważne. W jakiś sposób (uzasadniony statystycznie albo oparty wyłącznie na naszym przeczuciu) możemy niektóre kryteria premiować, a inne uważać za mało istotne. Stąd też mamy wektor wag, które powinny sumować się do 1.

Przykładowo: możemy uznać, iż marża netto jest objęta wagą 1/2, płynność bieżąca ma 3/5, a pozostałe 2/5 dzielą między siebie wszystkie pozostałe wskaźniki wymienione wcześniej. To oznaczałoby, że tak naprawdę przy ocenie biznesu interesuje nas głównie rentowność netto i płynność bieżąca. Oczywiście tak być nie musi: zresztą, na naszych łamach zwykle przyjmujemy jednakowe wagi, na wszelki wypadek nie faworyzując żadnego kryterium.

Wyjściowe oceny mają postać wartości funkcji K_k(xⁱ). Innymi słowy, i-ty wariant oceniamy według k-tego kryterium. Na przykład trzecia spółka na liście ma według drugiego kryterium (a jest nim, powiedzmy, rentowność operacyjna) wynik 7.5 proc. Znowuż druga spółka ma według trzeciego kryterium (np. zadłużenia) wynik 82 proc. (co oznacza, że 77 proc. jej pasywów stanowią długi, a tylko 18 proc. kapitał własny; jest to zresztą sytuacja raczej niebezpieczna).

Problem w tym, że dane te są wyrażone liczbami z różnych zakresów. Jak można zestawić marżę 3.5 proc. ze wskaźnikiem płynności bieżącej na poziomie 1,70 pkt, a tym bardziej z kwotą przychodów wynoszącą 2.25 mln zł?

Można temu zaradzić, normalizując dane, tzn. nakładając na nie taką funkcję, że uzyskane wartości będą mieścić się w przedziale [0, 1]. W przypadku metody SAW zwyczajowo stosuje się dwa podejścia do tego zagadnienia. Wpierw jednak zaznaczmy, że macierz wyników znormalizowanych oznaczać będziemy tak:

Jak jednak przeprowadzić tę normalizację? Zacznijmy od tego, że niektóre kryteria są tzw. stymulantami (kryteriami zyskowymi), a niektóre - destymulantami (kryteriami kosztowymi). Te pierwsze powinny przyjmować jak najwyższe wartości - np. płynność bieżąca czy rentowność netto powinny być jak najwyższe (to uproszczone założenie, ale można je roboczo przyjąć). Znowuż zadłużenie, co do zasady, powinno być jak najniższe - więc jest destymulantą.

Pierwszy z poniższych dwóch wzorów dotyczy stymulant, drugi destymulant (przy czym przyjmujemy, że wyjściowe wartości są nieujemne!):

Jak widać, każdą wartość o charakterze stymulanty - czyli wartość k-tego kryterium dla i-tego wariantu, o ile to kryterium jest stymulantowe - dzielimy przez najwyższą wartość w całej puli scenariuszy, oczywiście dla tegoż k-tego kryterium.

W drugim przypadku bierzemy najniższą wartość dla k-tego kryterium, o ile jest ono destymulantą - i dzielimy ją przez wartość dla ustalonego, i-tego scenariusza (tego, który teraz przetwarzamy).

Stosuje się też inne wzory, mianowicie takie:

Są one bardziej skomplikowane, ale nie wymagają założenia o nieujemności rezultatów. Są skonstruowane tak, że finalny wynik trafi, podobnie jak przy pierwszym sposobie, do [0, 1].

To już prawie wszystko. Prawie, bo wreszcie przechodzimy do clou zagadnienia. Oto główny wzór metody SAW:

Jak widać, dla każdego scenariusza obliczamy wartość p_i, a jest ona sumą znormalizowanych ocen zważonych uprzednio przyjętymi wagami. To wszystko. W zasadzie zagadnienie normalizacji jest nawet trudniejsze niż ów finalny wzór.

Intuicyjnie rzecz wydaje się sensowna: po prostu patrzymy, ile "punktów" zbiera każdy wariant, a każdy punkt to iloczyn wagi danego kryterium i oceny scenariusza według tegoż kryterium. Za najlepszy uważamy ten wariant, który uzyska najwięcej punktów. Za najsłabszy ten, który uzyska ich najmniej. Oczywiście niektóre scenariusze mogą zdobyć takie same wartości p_i. Wówczas metoda ta nie rozstrzyga o hierarchii takich wariantów i trzeba zastosować inne algorytmy MCDM (np. ARAS, COPRAS, MOORA, ELECTRE czy VIKOR).

Metoda SAW jest bardzo znana. Za pokrewną można uznać metodę WPM (Weighted Product Model), w której finalny wynik to nie suma zważonych ocen, ale ich iloczyn. Obie te metody w pewien sposób połączono w algorytmie WASPAS, również prezentowanym na naszych łamach.

Adam Witczak

BIBLIOGRAFIA:

"Wielokryterialne wspomaganie decyzji. Metody i zastosowania", red. T. Trzaskalik, Polskie Wydawnictwo Ekonomiczne 2014.

A. Kobryń, "Wielokryterialne wspomaganie decyzji w gospodarowaniu przestrzenią", Difin 2014.