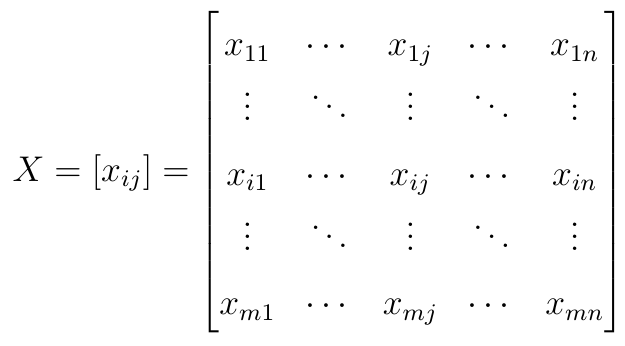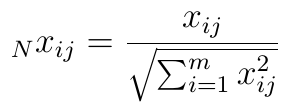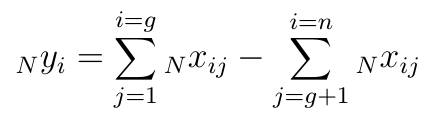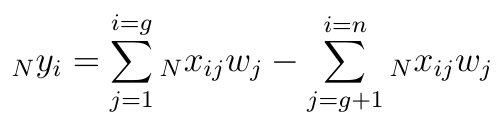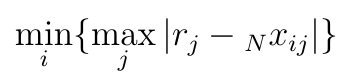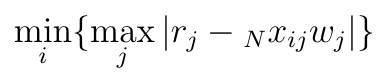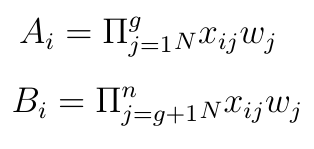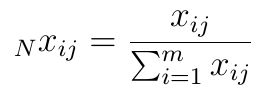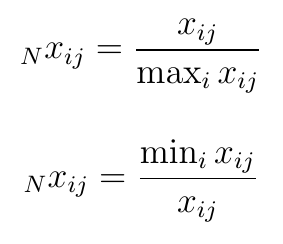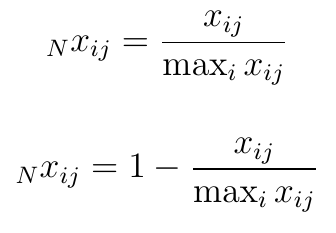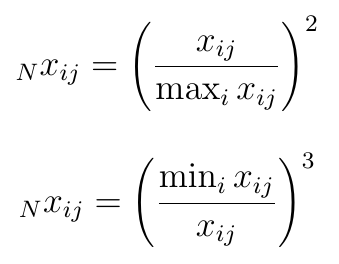Metoda wielokryterialna MOORA

Kontynuujemy przegląd wielokryterialnych algorytmów wspomagania decyzji. Tym razem będziemy mówić o metodzie MOORA, zaprezentowanej po raz pierwszy na łamach pisma 'Control and Cybernetics' w roku 2006.

MOORA to skrót od Multi-Objective Optimization on the basis of Ratio Analysis. Metodę opracowali W. K. Brauers z Uniwersytetu w Antwerpii oraz E. K. Zavadskas - litewski matematyk i informatyk, który współtworzył także wiele innych narzędzi wielokryterialnych (np. ARAS, COPRAS czy WASPAS).

Tak naprawdę MOORA to pakiet trzech metod, opartych na różnych sposobach myślenia. Jak to zwykle bywa w MCDM (multi-criteria decision making), punktem wyjścia jest macierz decyzji:

Mamy m wierszy (numerowanych indeksem i) oraz n kolumn (indeksowanych literką j). Idea jest taka: m alternatyw (np. możliwych do wyboru inwestycji), które badamy ze względu na n kryteriów. Ciekawostka: w pierwszym artykule nt. MOORA macierz była transponowana w stosunku do wyżej zapisanej, czyli kryteria były liczone wierszami, a scenariusze kolumnami. Naturalnie to tylko kwestia zapisu, zresztą później autorzy przeszli na bardziej typowe ujęcie.

Ze względu na pewne kwestie, które będą rozpatrywane później, możemy przyjąć, iż pierwszych g kolumn to stymulanty - czyli kryteria, które chcemy maksymalizować. Od g+1 do n mamy destymulanty, czyli kryteria, które uważamy za najlepsze, gdy osiągają najniższe wartości.

Dane, którymi dysponujemy, mogą być wyrażone w bardzo różnych skalach: dla każdego kryterium rząd wielkości może być zupełnie różny (np. rentowność rzędu kilku, kilkunastu procent, kwota przychodów w milionach zł itd.). Z tego powodu wszystkie liczby w macierzy należy znormalizować. W metodzie MOORA bazowo stosuje się następujący wzór (z pracy Van Delfta i Nijkampa z r. 1977):

To, dlaczego wybrano właśnie taki, leży poza zakresem naszego tekstu (odsyłamy do bibliografii). W każdym razie dane są już znormalizowane, wszystkie liczby należą do zakresu [0, 1]. Teraz możemy zrealizować pierwszą z trzech metod zawartych w pakiecie MOORA: Ratio System of MOORA.  

Otóż dla każdego i-tego scenariusza obliczamy następującą różnicę sum:

Innymi słowy, sumujemy znormalizowane wartości dla stymulant i destymulant (osobno), po czym drugą sumę odejmujemy od pierwszej. To wystarczy, by zbudować ranking naszych alternatyw: najlepszy jest scenariusz z najwyższym wynikiem, najgorszy ten z najniższym. Ustawiamy zatem obliczone rezultaty od najwyższego do najniższego.

Może być tak, że kryteria mają różną ważność: np. uważamy, że rentowność operacyjna spółki jest ważniejsza niż wskaźnik płynności bieżącej (lub odwrotnie). To, jak konstruować wagi w sposób bardziej obiektywny niż przeczucie decydenta, nie będzie nas tu zajmować (istnieją takie metody, oparte np. na statystyce). Zakładamy po prostu, że każde j-te kryterium ma swoją wagę w_j, a wszystkie wagi sumują się do 1. Wówczas ostatni wzór można zmodyfikować następująco:

Idea jest ta sama, tyle że uwzględniamy wagi. Ponownie: im wyższy ostateczny wynik (im więc mniejsza różnica sum), tym lepiej.

*

A teraz druga część metody MOORA: The Reference Point Approach (podejście oparte o punkt odniesienia). Wracamy do macierzy znormalizowanej i dla każdego j-tego kryterium obliczamy r_j - tj. najlepszy wynik (wynik spółki, która w tej kategorii wypadła najlepiej). Innymi słowy, jeśli naszym kryterium nr 1 jest rentowność netto, to patrzymy, w której spółce była ona najwyższa. W ten sposób dostajemy r₁. Jeżeli kategoria 2 to płynność bieżąca, wówczas szukamy spółki o najwyższej płynności i jej rezultat bierzemy jako r₂. I tak dalej - przy czym mamy dane znormalizowane w taki sposób, że różnica pomiędzy stymulantami a destymulantami się zatraciła. Im wyższy wynik, tym lepiej.

Następny ruch to wykorzystanie tzw. metryki mini-maxowej Czebyszewa. Poniżej widzimy jej formułę:<

Spróbujmy odczytać, co się tu dzieje. Badamy po kolei każdy i-ty scenariusz (np. spółkę z GPW). Przy ustalonym i (np. spółka nr 1, 2, 3, ...) sprawdzamy kryteria - od nr 1 do nr n. Przy każdym j-tym kryterium bierzemy r_j i obliczamy różnicę pomiędzy tą wzorcową, najlepszą wartością - a ij-tym wyrazem macierzy, czyli wartością j-tej cechy dla naszej i-tej spółki. Ściślej: rozważamy nie samą różnicę, a jej moduł (wartość bezwzględną), by wynik był dodatni.

Następnie bierzemy maksimum z uzyskanych wartości. Innymi słowy, jest pewna cecha (być może będzie ich kilka), według której nasza spółka jest najgorsza, najdalsza od wzorca - i tę właśnie odległość zapamiętujemy.

W ten sposób, jak powiedzieliśmy, badamy wszystkie scenariusze, a następnie z uzyskanych maksimów wybieramy minimum. Można to opisać tak: dla każdej spółki szukamy jej najsłabszego punktu. Dla jednej będzie to rentowność netto, dla innej wypłacalność natychmiastowa, dla jeszcze innej poziom zadłużenia. Następnie patrzymy, który z tych najsłabszych punktów jest mimo wszystko najsilniejszy. Spółka, którą w ten sposób odnajdziemy - jest najlepsza według tej części metody MOORA. Kolejna - jest nieco gorsza. I tak dalej, aż do ostatniej.

Oczywiście cechy (kryteria) mogą mieć różne wagi. Wówczas wzór wygląda tak:

Dalsze rozważania są takie same - szeregujemy podmioty od najmniejszego z maksimów do największego. Ten pierwszy jest najlepszy.

*

Trzecia część metody MOORA opiera się na iloczynach zważonych wartości znormalizowanych. Nazywa się to Full Multiplicative Form of MOORA.

Oblicza się dwa iloczyny, pierwszy dla stymulant, drugi dla destymulant. Wzory od razu podajemy w wersji z wagami:

Następnie oblicza się U_i, tj. całkowitą użyteczność (overall utility) każdej i-tej alternatywy. Jest to następujący iloraz:

Tak więc iloczyn stymulantowy dzielimy przez iloczyn destymulantowy. Im wyższy wynik, tym lepszy scenariusz.

*

Mamy zatem trzy rankingi. Możemy skorzystać tylko z jednego, możemy też w sposób mniej lub bardziej arbitralny je porównywać. W istocie twórcy MOORA opracowali też postępowanie MULTIMOORA, które w pewien usystematyzowany sposób pozwala wyłonić ostateczny ranking. Nie będziemy jednak omawiać tu tej techniki. Dość powiedzieć, że jest ona dostępna w pakiecie 'MCDM' dla języka R (wraz z innymi algorytmami, jak np. WASPAS, VIKOR czy TOPSIS).

*

Ktoś mógłby zapytać, czy ten rodzaj normalizacji zmiennych, jaki zastosowaliśmy, jest jedynym możliwym. Otóż nie. Istnieje wiele innych sposobów. W pracy "Comparative Analysis of Objective Techniques for Criteria Weighing in Two MCDM Methods on Example of an Air Conditioner Selection" Vujcica, Papica i Blagojevica zastosowano aż 6 wariantów, budując rankingi MOORA. Niektóre z nich zostały zresztą omówione już w pierwszej pracy Zavadskasa i Brauersa.

Mamy np. wzór Voogda:

Jest on podobny do wzoru Van Delfta, czyli naszego bazowego, ale sumuje się po prostu zmienne, a nie ich kwadraty - i nie bierze się pierwiastka.

Druga formuła przypisywana jest Weitendorfowi (właściwie to dwie formuły, pierwsza dla stymulant, druga dla destymulant):

Bardzo prosta opcja to wzory Stoppa (znów są dwa):

Jak widać, w przypadku stymulant dzielimy badany wynik przez najlepszy według testowanego kryterium, a w przypadku destymulant dzielimy rezultat najlepszy (czyli najniższy) przez aktualnie badany.

Dość podobne są wzory Koertha:

Na koniec mamy nieliniowe formuły normalizacyjne Peldschusa:

To nie błąd: twórca tych wzorów rzeczywiście uważa, iż w przypadku destymulant powinno się zastosować trzecią potęgę, a drugą w przypadku stymulant. Naturalnie nie będziemy zagłębiać się w sens tego podejścia ani w ogóle w wymowę zaprezentowanych formuł. Tematy te są jednak badane w pracach naukowych i każda z tych normalizacji ma pewne ograniczenia oraz pewne zalety.


Adam Witczak


BIBLIOGRAFIA:

J. Antucheviciene, E. K. Zavadskas, J. Saparauskas, Z. Turskis, "MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions", Economic Computation and Economic Cybernetics Studies and Research, 47(2), January 2013.

W. K. M. Brauers, E. K. Zavadskas, "MULTIMOORA optimization used to decide on a bank loan to buy property", Technological adn Economic Development of Economy, Vol. 17(1) 2011.

W. K. M. Brauers, E. K. Zavadskas, "Project Management by MULTIMOORA as an instrument for transition economies", Technical and Economic Development. Baltic Journal on Sustainability, Vol. 16(1) 2010.

W. K. M. Brauers, E. K. Zavadskas, "The MOORA Method and its Application to Privatization in a Transition Economy", Control and Cybernetics 35(2), 445–469.

N. Kundakci, "Combined multi-criteria decision making approach based on Macbeth and Multi-Moora Methods", Alphanumeric Journal, vol. 4, Issue 1, 2016.

M. Vujcic, M. Papić, M. D. Blagojević, "Comparative Analysis of Objective Techniques for Criteria Weighing in Two MCDM Methods on Example of an Air Conditioner Selection", Tehnika-Menadzment 67 (2017).