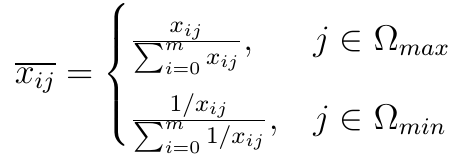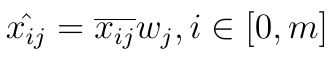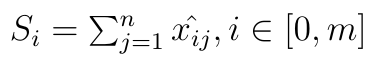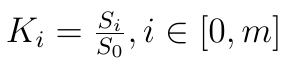O rankingu według metody ARAS

ARAS to prosta metoda wielokryterialna, która została po raz pierwszy zaprezentowana w roku 1996 przez naukowców z Litwy: E. K. Zavadskasa i Z. Turskisa. Należą oni do swego rodzaju zespołu badawczego, który opracował także inne algorytmy MCDM, np. WASPAS czy COPRAS.

Akronim ARAS rozwija się następująco: Additive Ratio Assesment (method). Zaprezentujemy kroki tego schematu, bazując - jeśli chodzi o terminologię i wzory - przede wszystkim na oryginalnej pracy wspomnianych wcześniej autorów ("A new additive ratio assessment (ARAS) method in multicriteria decision-making") oraz na opracowaniu D. Stanujkica, B. Dordevica i M. Dordevica "Comparative Analysis of Some Prominent MCDM Methods: A Case of Ranking Serbian Banks".

Rzecz zaczyna się standardowo - od budowy macierzy decyzyjnej (decision-making matrix, DMM). Innymi słowy, mamy m scenariuszy i n kryteriów. Przykładowo, scenariuszami (alternatywami) mogą być nieruchomości, w które chcemy zainwestować. Wówczas kryteria to np. cena za metr kwadratowy, powierzchnia, całkowita cena, stan techniczny (określony mniej lub bardziej arbitralnie w punktach), wiek budynku itd.

Bazowa macierz wygląda zatem następująco:

Element x_ij to ocena i-tego scenariusza według j-tego kryterium. Na przykład x₂₅ oznaczałoby, według przyjętych wyżej oznaczeń, wiek drugiej z rozpatrywanych nieruchomości.

Zauważmy (choć to tylko kwestia notacji), że najwyższy wiersz macierzy jest "zerowy" (podczas gdy kolumny liczone są od "pierwszej"). Otóż w owym wyróżnionym, zerowym wierszu mamy tzw. wariant optymalny czy też wzorcowy, z którym będziemy później porównywać nasze scenariusze. Skąd się on bierze? W pewnym sensie jest dowolny. To znaczy: możemy arbitralnie określić, jakie wartości kolejnych kryteriów uważamy za najlepsze. Bazować możemy np. na najlepszych wartościach z puli wyborów znacznie szerszej niż ta, którą my sami się posługujemy, nawet z całej puli rynkowej. Przykładowo: mając do dyspozycji dziesięć nieruchomości, za ideał ceny metra kwadratowego uznamy najniższą cenę spotykaną w całym województwie czy wręcz kraju, choć oczywiście z różnych przyczyn nie mamy możliwości kupić dowolnego obiektu na całym tym terenie.

Jeżeli jednak nie mamy jakichś zewnętrznych poszlak, to możemy zastosować podejście bardzo typowe dla metod MCDM:

Po pierwsze, odnosimy się tu tylko do naszej puli scenariuszy, poczynając od wiersza nr 1. Po drugie, kryteria dzielą się na dwa zbiory: Ω_max i Ω_min. Pierwszy to stymulanty - chcemy, aby wartości były to jak najwyższe. Drugi to destymulanty, powinny być one jak najniższe. Przykładowo, przy ocenie spółki giełdowej zadłużenie zazwyczaj traktuje się jako destymulantę, a rentowność netto czy płynność bieżącą jako stymulantę. Można też mówić o optymalnych zakres i jest to nawet bardziej sensowne, ale i bardziej pracochłonne.

A zatem przeglądamy wszystkie scenariusze po wszystkich kryteriach i do wektora wzorcowego wrzucamy najlepsze wartości kryteriów.

Jest jeszcze jeden problem. Nasze dane prawdopodobnie nie są znormalizowane. To znaczy: są dane różnymi jednostkami i obejmują wielkości różnej skali. W niektórych metodach MCDM, jak np. algorytm Bordy, nie gra to roli, ale tutaj tak. Nie możemy porównywać rentowności netto 27 proc. z płynnością bieżącą 1,35 pkt i przychodami rocznymi w wysokości 12,5 mln zł.

Z tego powodu dane są normalizowane. Można to zrobić na różne sposoby, ale bazowo autorzy ARAS przyjęli następujące wzory transformacji liniowej przy pomocy sumy:

Jak widać, w zależności od tego czy rozważamy stymulantę czy destymulantę, bierzemy iloraz wartości (lub jej odwrotności) przez sumę wartości (lub ich odwrotności) po scenariuszach przy ustalonym kryterium. Wynik trafi do [0, 1]. Wzory są zbudowane tak, że teraz wszystkie kryteria mają charakter stymulant.

Mamy już więc macierz wartości znormalizowanych:

Być może jednak nie wszystkie kryteria są dla nas tak samo ważne. Na przykład możemy uważać, że stan techniczny budynku jest mało istotny, ważne natomiast, by był on dobrze położony - albo też, by metr kwadratowy kosztował niewiele.

Z tego powodu każde kryterium otrzymuje swoją wagę w_j. Wagi te powinny sumować się do 1:

Teraz bierzemy nasze znormalizowane dane i uwzględniamy wagi, generując elementy macierzy znormalizowanej i zważonej:

Spójrzmy na kolejną formułę:

Mówi ona, że dla każdego scenariusza (w tym dla wzorcowego) obliczamy wartość tzw. funkcji optymalności (optimality function). Innymi słowy, sumujemy wyniki dla poszczególnych alternatyw. Im wyższa taka suma, tym lepiej świadczy to o danym scenariuszu. Już samo to szereguje nam w jakiś sposób rozważane opcje, ale obliczamy jeszcze tzw. stopień alternatywnej użyteczności (the degree of the alternative utility) każdej alternatywy:

Innymi słowy, mierzymy stosunek każdego scenariusza do modelu wzorcowego (wynik trafia do [0, 1]). A zatem mamy tu coś więcej niż mieliśmy w poprzednim kroku, kiedy po prostu mogliśmy ułożyć (np. rosnąco) wartości S_j. Teraz widzimy, jak "dobre" są nasze opcje w stosunku do ideału. Teoretycznie może się np. okazać, że nawet najlepszy z faktycznych scenariuszy jest bardzo kiepski w porównaniu z pożądanym przez nas wzorcem. Być może wtedy należy w ogóle zrezygnować z inwestycji i poczekać na lepsze oferty?

Ostatecznie możemy rozważane alternatywy uszeregować rosnąco lub malejąco według wartości K_i. W ten sposób dowiemy się, która opcja jest "najlepsza", która "najgorsza" i jak są poukładane pomiędzy nimi pozostałe scenariuszy. Nie bez powodu stosujemy cudzysłowy: jak zwykle w świecie MCDM trzeba pamiętać, że alternatywy są dobre i złe tylko według dane metody... Algorytmy TOPSIS, ELECTRE czy VIKOR mogłyby dać inny ranking. Gdyby jednak dały (wszystkie) taki sam lub gdyby ich oceny były podobne, wówczas uwiarygadniałoby to sensowność całego przedsięwzięcia.

Metoda ARAS nie jest skomplikowana (nawet przy ręcznym liczeniu, a przecież dysponujemy oprogramowaniem komputerowym). Wypada jednak dodać, że zbudowano jej rozszerzenia oparte na (trójkątnych) liczbach rozmytych oraz na teorii zbiorów (liczb) szarych (grey sets / numbers), opracowanej w latach 80-tych przez chińskiego matematyka Denga. Odpowiednie artykuły czytelnik znajdzie w bibliografii, a my i tak zajmiemy się tymi rozszerzeniami w kolejnych artykułach.

Adam Witczak


BIBLIOGRAFIA:

D. Stanujkic, B. Dordevic, M. Dordevic, "Comparative Analysis of Some Prominent MCDM Methods: A Case of Ranking Serbian Banks", Serbian Journal of Management 8 (2) (2013) 213 - 241.

D. Stanujkic, "Extension of the ARAS Method for Decision-Making Problems with Interval-Valued Triangular Fuzzy Numbers", INFORMATICA, 2015, Vol. 26, No. 2, 335 - 355.

E. K. Zavadskas, Z. Turskis, "A new additive ratio assessment (ARAS) method in multicriteria decision-making", Technological and Economic Development of Economy, 2010, 16(2): 159 - 172.

E. K. Zavadskas, Z. Turskis, "A Novel Method for Multiple Criteria Analysis: Grey Additive Ratio Assessment (ARAS-G) Method", INFORMATICA, 2010, Vol. 21, No. 4, 597 - 610.