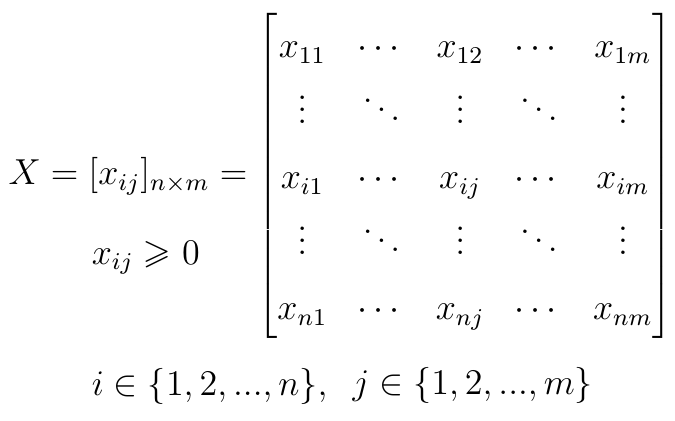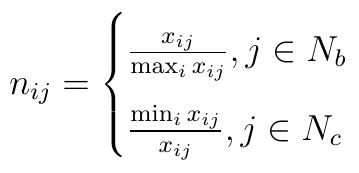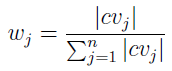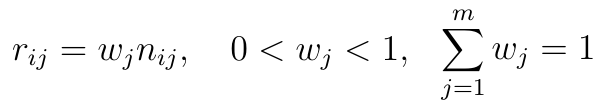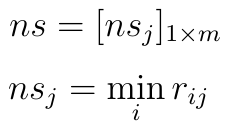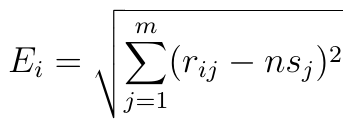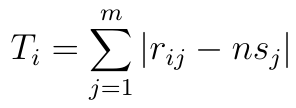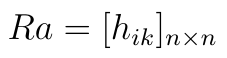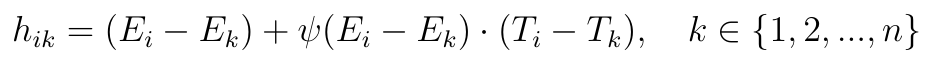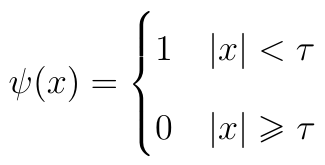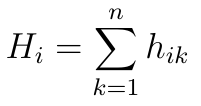Metoda wielokryterialna CODAS

CODAS to wielokryterialna metoda podejmowania decyzji, która została wprowadzona w pracy zespołu badaczy z Iranu i Litwy, zatytułowanej "A New Combinative Distance-Based Assessment (CODAS) Method For Multi-Criteria Decision-Making".

Praca ta ukazała się zupełnie niedawno, bo w roku 2016, na łamach czasopisma "Economic Computation and Economic Cybernetics Studies and Research". W gronie autorów jest m.in. prof. E. K. Zavadskas, współautor wielu algorytmów MCDM, z których część prezentowaliśmy na naszych łamach (np. ARAS, COPRAS czy WASPAS). Inne dopiero się pojawią: np. EDAS.

COmbinative Distance-Based ASsessment - tak się rozwija skrót CODAS. Algorytm należy do klasy tych, które bazują na pomiarze odległości pomiędzy scenariuszem (w naszym przypadku będą to najczęściej spółki giełdowe, badane pod kątem wskaźników bilansowych) - a pewnym wzorcem. Wzorzec to pewna spółka hipotetyczna, wyobrażona czy też skonstruowana na bazie dostępnych danych. Zazwyczaj jest to spółka idealna: polega to na tym, że dla każdego kryterium bierzemy najlepszy z dostępnych wyników, tzn. wynik spółki najlepszej w tej konkurencji. Często (tak jest np. w TOPSIS) równolegle buduje się kontr-ideał (antyideał, wzorzec negatywny), tj. spółkę najgorszą. Z kolei w EDAS mierzy się odległość badanych scenariuszy od scenariusza uśrednionego.

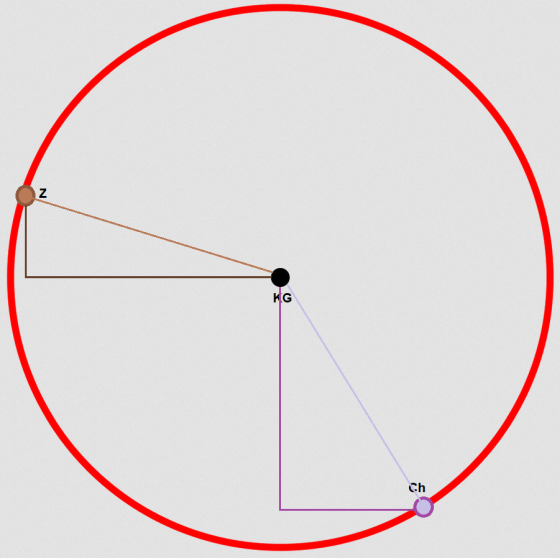
W CODAS interesuje nas ideał negatywny. Co jest charakterystyczne dla tej metody? Otóż najpierw sprawdza się tu odległość scenariusza (spółki) od tegoż ideału negatywnego, a ten dystans oblicza się przy pomocy metryki euklidesowej. To ta metryka, którą uważamy za najbardziej intuicyjną: pierwiastek kwadratowy z sumy kwadratów różnic wartości odpowiednich współrzędnych. Odległość euklidesową pomiędzy dworcem Zabrze a dworcem Katowice Główne można rozumieć (oczywiście w pewnej skali, chyba że dysponowalibyśmy naprawdę dużym cyrklem...) tak: wbijamy cyrkiel w Katowicach i kreślimy taki okrąg, który będzie przechodzić przez Zabrze. Nasz dystans to długość promienia łączącego (dworzec) Zabrze z Katowicami.

Powstaje jednak pewien problem: wszystkie punkty na tym okręgu mają taką samą odległość. W szczególności np. dworzec w miejscowości Chełm Śląski (tak naprawdę jest oczywiście pewna różnica, ale minimalna: w przybliżeniu jest tak daleko od KG jak Zabrze). Zatem w świetle metryki euklidesowej te punkty są nieporównywalne: są identyczne. Te, które tylko minimalnie odbiegają od okręgu, są bardzo podobne, co też jest kłopotliwe.

Można jednak skorzystać z innych metryk. Jedną z nich jest tzw. odległość taksówkowa (taxicab). Jej istotę wyjaśnijmy korzystając z rysunku:

Jasnymi odcinkami zaznaczyliśmy odległości euklidesowe, czyli promienie okręgu. Ciemnymi - odległości taksówkowe. Jak można się domyślić, w tym wypadku nie są one sobie równe (czytelnik może się zastanowić: kiedy byłyby równe sobie i kiedy byłyby równe odpowiadającym sobie odległościom euklidesowym?).

*

Idea metody CODAS jest taka: szukamy scenariusza najgorszego, ideału negatywnego. Sprawdzamy, jak daleko każdy scenariusz (każda spółka) jest od tego najgorszego w sensie euklidesowym. Jeśli różnica jest zerowa lub bardzo mała (co to znaczy "bardzo mała", to już musimy sobie mniej lub bardziej arbitralnie ustalić), wtenczas dodatkowo korzystamy z metryki taksówkowej i na tej podstawie budujemy finalny ranking. Im spółka dalej od kontr-ideału, tym lepsza (i vice-versa).

Prześledźmy teraz konkretne kroki tej procedury. Mamy n scenariuszy oraz m kryteriów. Zapisujemy to w macierzy decyzyjnej X:

Element x_ij opisuje wynik i-tej alternatywy w świetle j-tego kryterium.

Dane mogą być jednak w różnych jednostkach i zakresach. Dlatego normalizujemy je tak, by mieściły się w zakresie [0, 1] - i zarazem tak, by wyższe wartości były tymi lepszymi.

Przez N_b rozumiemy kryteria benefitowe, tj. stymulanty. To znaczy takie, co do których sądzimy, iż dobrze, gdy przyjmują wysokie wartości. W naszych analizach większość kryteriów (wskaźników) ma taki charakter: np. uznajemy (co jest trochę nieścisłe, ale od uproszczeń nigdy nie uciekniemy), że płynność bieżąca powinna być jak najwyższa; że najlepsze są najwyższe poziomy marży netto czy marży operacyjnej; że preferujemy wysokie wartości ROE i ROA. Jak widać, w takiej sytuacji dzielimy po prostu badaną wartość przez najlepszą wartość według rozważanego kryterium. Jeśli np. 3-cia z 10 spółek ma płynność bieżącą 1,25 pkt, a rekordowa płynność w tej puli firm to 3,25 pkt, wówczas 3-ciej przypiszemy znormalizowaną wartość 1,25 / 3,25 = 0,385 pkt (w przybliżeniu). Spółka o płynności 2,15 pkt dostanie 0,661 pkt.

N_c to zbiór tych kryteriów, które są destymulantami. Im niższe, tym lepiej. To na przykład zadłużenie. Po normalizacji jednak interpretuje się je tak samo jak stymulanty. Wyobraźmy sobie, że 3-cia spółka ma zadłużenie 65 proc. sumy bilansowej (0,67 pkt), 5-ta spółka tylko 33 proc., a najniższe zadłużenie w całej puli to 24 proc. Wówczas spółka nr 3 dostaje 0,24 / 0,65 = 0,369 pkt, a firma nr 5 otrzymuje 0,24 / 0,33 = 0,727 pkt (a więc wyższy wynik).

Oczywiście ten sposób normalizacji nie jest czymś szczególnym: używa się go przy wielu innych metodach MCDM. Zresztą, można sobie wyobrazić wykorzystanie innego typu normalizacji lub standaryzacji (zagadnieniom tym poświęciliśmy odrębny tekst).

Kryteria mogą mieć równą wagę, ale nie muszą: to znaczy, niektóre możemy uważać za istotniejsze od innych. To trochę uznaniowe, choć istnieją metody matematyczne, które pozwalają wprowadzić tu pewną systematyzację. Jeżeli nie mamy lepszego pomysłu, można kryteria uznać za jednakowo istotne - albo przyjąć, że najważniejsze są te, które mają najwyższy wskaźnik zmienności. W tym drugim przypadku j-temu kryterium przypiszemy taką wagę w_j:

Otóż cvj to właśnie współczynnik zmienności (coefficient of variation) poziomu realizacji wariantów dla j-tego kryterium. Jeśli np. wszystkie spółki mają bardzo podobną płynność bieżącą, np. w zakresie 1,20 - 1,40 pkt, a jednocześnie wypłacalność natychmiastowa przyjmuje wiele różnych wartości w zakresie od 0,02 pkt do 1,10 pkt, wtedy zapewne wyjdzie nam, że kryterium wypłacalności jest istotniejsze od ogólnej płynności. Wagi te można przeliczyć przed normalizacją.

W każdym razie, jeśli mamy już wagi, to wyliczamy znormalizowane wyniki, tj. dla każdej i-tej spółki i każdego j-tego kryterium realizujemy formułę:

Wagi powinny być ułamkami z zakresu (0, 1), które sumują się do 1.

Teraz określamy negatywny ideał:

A więc ns to scenariusz (firma) określony wektorem takim, że dla każdego kryterium wybieramy najgorszy wynik z puli rezultatów zważonych i znormalizowanych.

W następnym kroku obliczamy odległość euklidesową każdej alternatywy (scenariusza) od tego kontr-ideału:

Liczymy również dystans w sensie taksówkowym:

Jak widać, formuła polega na tym, że bierzemy moduły (a nie kwadraty) różnic pomiędzy wartościami na odpowiednich współrzędnych, sumujemy je... i nie wyciągamy już oczywiście pierwiastka.

Formujemy jeszcze jedną macierz. Tym razem taką:

To właśnie clou metody CODAS. Zobaczmy, co umieszczamy w macierzy. Ma ona rozmiar n x n. To znaczy, że teraz badamy zależności pomiędzy i-tą i k-tą spółką (pomiędzy każdą parą scenariuszy). Dla każdej pary obliczamy h_ik:

Ten z kolei wzór składa się z dwóch składników. Pierwszy to różnica odległości euklidesowych obu firm od wzorca negatywnego, tj. E_i - E_k. Drugi to iloczyn różnic odległości taksówkowych oraz pewnej szczególnej funkcji ψ. Ta zaś jest definiowana następująco:

Otóż τ to pewien parametr progowy. Powinna być to wartość bliska zeru. To tak jakby zakres nietolerancji. Zauważmy, że jako x, jako argument funkcji ψ, stosujemy E_i - E_k. A zatem: jeśli różnica pomiędzy euklidesową odległością i-tej spółki od ns a euklidesową odległością k-tej spółki od ns jest niewielka, czyli jeśli obie są w bardzo podobnej odległości od ns, to wtedy ψ przyjmuje wartość 1. Wtedy nasz wzór przybiera postać: h_ik = (E_i - E_k) + (T_i - T_k). To właśnie idea, którą wcześniej sygnalizowaliśmy: jeżeli alternatywy są nieporównywalne euklidesowo (albo "bardzo kiepsko porównywalne"), to uciekamy się do metryki taksówkowej, która może nam pomóc.

Co do τ, to autorzy pierwotnej pracy korzystali z wartości 0,02 pkt. Może być ona trochę inna, nie będzie problemem eksperymentowanie z wartościami typu 0,01 pkt czy 0,05 pkt.

A teraz ostatni krok, przygotowanie końcowego rankingu. Każdej i-tej spółce przypisujemy wartość H_i:

A zatem to suma wartości h_ik dla tej spółki. To znaczy: suma różnic pomiędzy E_i i E_k (gdzie E_k jest liczone dla każdej innej spółki), powiększonych być może w niektórych przypadkach o T_i - T_k.

Uzyskane wyniki układamy w porządku malejącym. Najwyższy rezultat będzie tym najlepszym, najniższy - najgorszym.

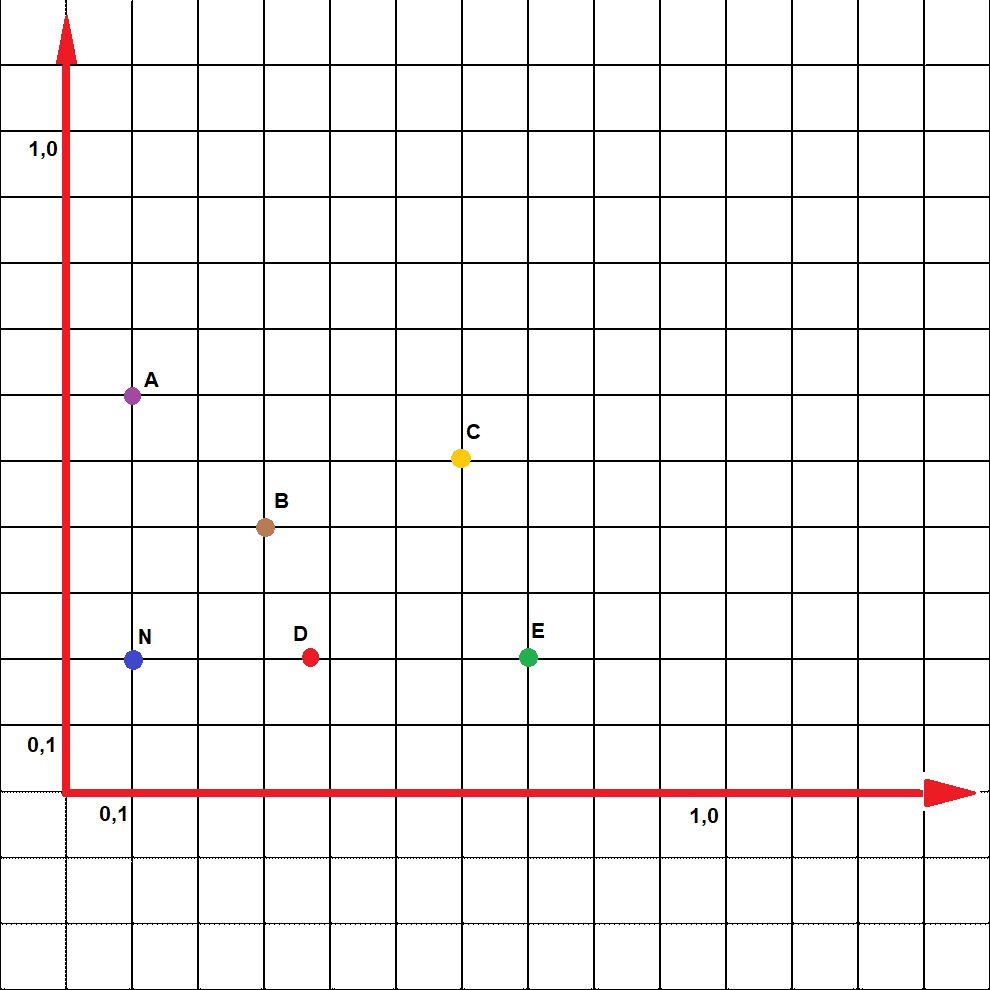
Metodę CODAS będziemy stosować przy analizie spółek w odrębnych artykułach. Na razie zaprezentujemy prosty przykład zbudowany na dość abstrakcyjnych danych. Spójrzmy na rysunek:

Mamy pięć scenariuszy: A, B, C, D, E. Rozpatrujemy je pod kątem dwóch kryteriów. Po wykonaniu podstawowych obliczeń (ważenie, normalizacja itd.) otrzymaliśmy negatywny scenariusz N = [0.1, 0.2]. Wyniki pozostałych scenariuszy to:

A = [0.1, 0.6] (właśnie z A została wybrana do N wartość pierwszego kryterium)

B = [0.3, 0.4]

C = [0.6, 0.5]

D = [0.375, 0.2]

E = [0.7, 0.2] (wartość drugiego kryterium w N została wzięta z E lub równoważnie z D)

Odległości euklidesowe tych punktów od N prezentują się tak:

E_A = 0.4

E_B = sqrt((0.3 - 0.1)^2 + (0.4 - 0.2)^2) = sqrt(0.2 ^ 2 + 0.2 ^ 2) = sqrt(0.08) = ok. 0.283.

E_C = sqrt((0.6 - 0.1)^2 + (0.5 - 0.1)^2) = sqrt(0.25 + 0.16) = sqrt(0.41) = ok. 0.640.

E_D = 0.375 - 0.1 = 0.275.

E_E = 0.6

Załóżmy, że nasz próg τ to 0,02. Jedyna różnica mniejsza od tego progu (do do wartości bezwzględnej) to różnica E_B - E_D = 0.283 - 0.275 = 0.008. Raz jeszcze przypomnijmy: mówiąc o różnicach, mamy na myśli nie odległości pomiędzy punktami, ale różnice pomiędzy ich odległościami do N.

W takim razie dla pary (B, D) liczymy jeszcze metryki taksówkowe i różnicę pomiędzy nimi.

T_B = 0.2 + 0.2 = 0.4

T_D = 0.375

T_B - T_D = 0.4 - 0.375 = 0.025.

Teraz trzeba obliczyć h_ik:

h_AB = E_A - E_B = 0.117; h_AC = -0.24; h_AD = 0.125; h_AE = -0.2

h_BA = 0.283 - 0.4 = -0.117; h_BC = -0.357; h_BD = 0.008 + 0.025 = 0.033; h_BE = -0.317

h_CA = 0.24; h_CB = 0.357; h_CD = 0.365; h_CE = 0.04

h_DA = -0,125; h_DB = -0.008 - 0.025 = -0.033; h_DC = -0.365; h_DE = -0.325

h_EA = 0.2; h_EB = 0.317; h_EC = -0.04; h_ED = 0.325

I wreszcie finalne wartości H_i:

H_A = 0.117 - 0.24 + 0.125 - 0.2 = -0.198

H_B = -0.758

H_C = 1.002

H_D = -0.848

H_E = 0.802

Im wyższa wartość tym lepiej. Zatem ranking od najlepszej do najgorszej alternatywy jest taki: C, E, A, B, D. Czyli C to scenariusz najlepszy, a choć B i D są bardzo podobne z uwagi na metrykę euklidesową, to jednak po dokonaniu poprawki taksówkowej okazuje się, że B jest nieco lepszy niż D. Zarazem scenariusz D trafia na ostatnie miejsce rankingu. Te końcowe oceny wydają się zgodne z naszą intuicją: "na oko" C i E są najdalej od anty-wzorca, zaś pozostałe trzy scenariusze znacznie bliżej; ale jednocześnie A "nadrabia" dobrą wartością drugiego kryterium.

Adam Witczak

BIBLIOGRAFIA:

M. Keshavaraz Ghorabaee, E. K. Zavadskas, J. Antucheviciene, Z. Turskis, "A New Combinative Distance-Based Assessment (CODAS) Method for Multi-Criteria Decision Making", Economic Computation and Economic Cybernetics Studies and Research, Issue 3/2016, Vol. 50

I. A. Badi, A. M. Abdulshahed, A. G. Shetwan, "Supplier Selection Using Combinative Distance-Based Assessment (CODAS) Method For Multi-Criteria Decision Making", Proceedings of The 1st International Conference on Management, Engineering and Environment (ICMNEE) (pp. 395-407). Belgrade: ECOR (RABEK), 2017.

D. Pamucar, I. Bardi, K. Sanja, R. Obradović, "A Novel Approach for the Selection of Power-Generation Technology Using a Linguistic Neutrosophic CODAS Method: A Case Studyin Libya", Energies 2018, 11.