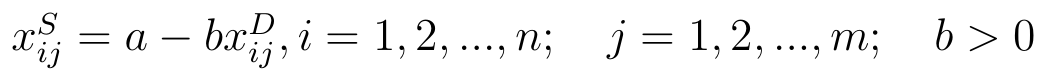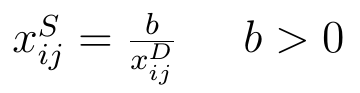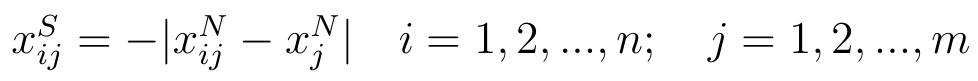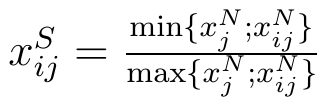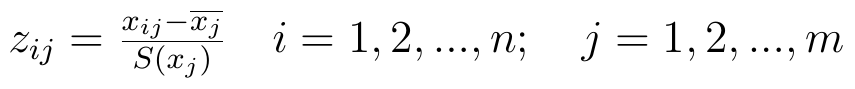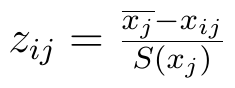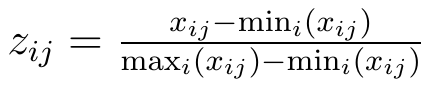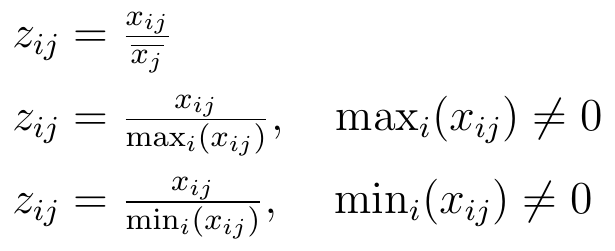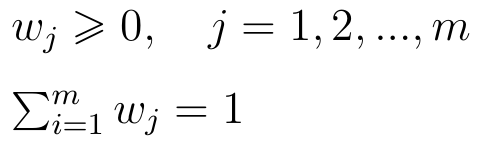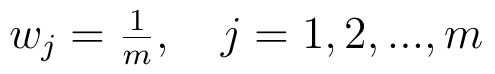Normalizacja zmiennych

Normalizacja i ważenie zmiennych to szerokie zagadnienie, które przedstawimy dziś jedynie w podstawowej formie. Zresztą, przewijało się już ono na naszych łamach - głównie przy okazji omawiania metod wielokryterialnych. Z tej perspektywy będziemy patrzeć na ten problem także i teraz.

Przypomnijmy: algorytmy typu MCDM (multi-criteria decision making) polegają w największej ogólności na tym, że mamy pewną liczbę scenariuszy do wyboru - i pewną liczbę cech, czy też kryteriów. Na przykład: spółki giełdowe z sektora transport i logistyka (obecnie jest ich na GPW siedem) oraz obliczone dla nich wskaźniki finansowe (takie jak płynność bieżąca, poziom zadłużenia, rentowność operacyjna czy roczny zwrot z kapitału). Na ogół na oko trudno określić, która firma jest najlepsza, a która najgorsza, a tym bardziej trudno uszeregować te, które są pomiędzy skrajnościami. Jedna firma ma lepszą marżę netto niż druga, ale znacznie gorszą płynność bieżącą itd.

Z tego powodu stosuje się metody takie jak np.:

- SAW (metoda średniej ważonej)
- MOORA (Multi-Objective Optimization on the basis of Ratio Analysis)
- COPRAS (COmplex PRoportional ASsesment)
- ARAS (Additive Ratio Assesment)
- WASPAS (Weighted Aggregated Sum Product Assessment)
- SPR-2T
- VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje)
- algorytm Bordy
- ELECTRE (ELiminiation Et Choix Traduisant la REalite)
- TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution)
- TMAI (Taksonomiczna Miara Atrakcyjności Inwestowania).

W większości z tych metod (choć nie we wszystkich) dane, które mamy na wejściu, trzeba w pewien sposób przetworzyć (nim przejdzie się do realizacji właściwego algorytmu). To przetworzenie jest potrzebne z kilku powodów:

1) niektóre cechy to stymulanty, tj. są dobre, gdy są jak najwyższe; inne to destymulanty (czyli preferujemy wartości jak najniższe); jeszcze inne to nominanty - w ich przypadku za najlepszą uważa się pewną szczególną wartość optymalną, ani minimum, ani maximum. Teoretycznie może to być również pewien zakres.

2) dane mogą być wyrażone w rozmaitych jednostkach i należeć do zupełnie różnych zakresów liczbowych: jak można równocześnie brać pod uwagę rentowność operacyjną 13 proc. i wskaźnik płynności bieżącej 1,75 pkt?

3) cechy niekoniecznie są jednakowo istotne; możemy np. uważać, że kluczowe przy ocenie spółki są rentowność operacyjna i zwrot z kapitału, a wszystkie pozostałe wskaźniki uważać za mało ważne. Innymi słowy, danym nadajemy pewne wagi.

*

W niektórych algorytmach MCDM już na początku przekształca się nominanty i destymulanty w stymulanty. Potem obliczenia są prostsze: zawsze pożądana jest maksymalizacja zmiennej, bez zbędnych dywagacji.

Otóż destymulantę w stymulantę przetworzyć można np. na poniższe dwa sposoby:

- różnicowy:

- ilorazowy:

W pierwszym wypadku a i b to pewne stałe. Często przyjmuje się, że b = 1, zaś a = 0 lub a to max_i (x_ij^D). Jeśli a = 0 i b = 1, to znaczy, że po prostu zmieniamy znak przy destymulancie. Jeśli np. za destymulantę uznamy zadłużenie i dla jakiejś firmy wyniesie ono 87 proc. (co można uznać za wartość wysoką, a więc złą), to wówczas będziemy tak naprawdę posługiwać się wartością -87 (proc.). Teraz to stymulanta: im ona wyższa, tym bliższa zeru, więc np. -15 będzie odpowiadać 15-procentowemu zadłużeniu, niskiemu.

Przy transformacji ilorazowej za b przyjmuje się na ogół 1. Wówczas w miejsce 87 proc. mieliśmy 1/87. Znów: im wyższy przekształcony wynik, tym lepsze (niższe) wyjściowe zadłużenie.

W przypadku nominant wzory wyglądają tak:

- wersja różnicowa:

- wersja ilorazowa:

Przez x_j^N rozumiemy wartość wzorcową czy też pożądaną naszej cechy. Na przykład możemy uznać, że idealna płynność bieżąca to 2,00 pkt. To z kolei może wynikać np. z przyjęcia, że tak naprawdę premiujemy cały przedział 1,50 - 2,50 pkt, ale dla wygody bierzemy jego środek.

Dodajmy, że wzory ilorazowe stosujemy tylko przy skalach ilorazowych, tzn. wtedy, gdy skala danych jest przedziałowa, ale do tego posiada zero absolutne. Tak np. jest z temperaturą w kelwinach, w odróżnieniu od skali Celsjusza.

Zauważmy, jak działa wzór drugi: bierzemy naszą, badaną wartość oraz poziom idealny i bierzemy mniejszą z tych liczb, a potem większą z nich. Jeśli np. x_ij^N > x_j^N, czyli nasza wartość jest zbyt duża, to wynikiem jest proporcja x_j^N / x_ij^N, czyli będziemy pracować z liczbą, która mówi nam, jaką częścią badanej wartości jest wartość pożądana. Jeśli x_ij^N < x_j^N, to uzyskamy wynik x_ij^N / x_j^N, czyli mówiący, jaką częścią wartości pożądanej jest nasz odczyt. Tak przetworzone dane to już stymulanty: im wyższa wartość ułamka, tym bliższa będzie 1, a 1 oznaczałoby tożsamość wartości cechy z ideałem.

*

Drugie zagadnienie to normalizacja zmiennych. Chodzi o ujednolicenie rzędów wielkości i pozbawienie danych mian, tj. doprowadzenie do tego, byśmy pracowali z "podobnymi" do siebie liczbami, a nie np. z procentami, punktami, dolarami czy tysiącami franków.

Otóż można do tego podejść od strony standaryzacji. Wszystkie wartości x_ij zmienia się tak, o ile są stymulantami:

Dla destymulant wzór jest taki:

Przez x_j z nadkreślnikiem rozumiemy średnią arytmetyczną j-tej zmiennej, czyli np. średnią płynność w puli badanych spółek; przez S(x_j) rozumiemy odchylenie standardowe tejże j-tej zmiennej. Otóż po standaryzacji zmienna będzie mieć wariancję 1 i średnią 0. Niektóre liczby staną się z dodatnich ujemne (o tym, że to możliwe, świadczy licznik ułamka: wystarczy, że trafimy na wartość mniejszą od średniej).

Inne podejście to tzw. unitaryzacja. Wariancje i średnie zmiennych (cech) pozostaną różne od siebie, ale za to wszystkie te cechy przyjmą wartości z wygodnego do obliczeń przedziału [0, 1]. Nierzadko stosuje się taką formułę (załóżmy, że pracujemy już z samymi stymulantami):

Tak więc od wartości badanej (czyli j-tej cechy i-tego obiektu, np. rentowności netto i-tej rozważanej spółki) odejmujemy najmniejszą wartość w puli i wynik dzielimy przez rozstęp, tj. różnicę między maximum a minimum. Przypuśćmy np., że najniższa rentowność netto w puli badanych firm to 6 proc. (0,06), najwyższa to 19 proc. (0,19), a w spółce o numerze i mamy akurat rentowność 13 proc. (0,13). Wtedy uzyskamy wynik: (0,13 - 0,06)/(0,19 - 0,06) = 0,07 / 0,13 = 0,54 (w przybliżeniu). Ma to sens, bo "na oko" nasza spółka jest mniej więcej "w połowie drogi" między skrajnościami.

Inne podejście to przekształcenie ilorazowe. Tutaj wartość badanej cechy przyrównuje się do pewnej ustalonej liczby, zwykle w jakiś sposób powiązanej z wartościami tej cechy dla pozostałych obiektów. Świadczą o tym poniższe wzory:

Są więc przynajmniej trzy możliwości: porównanie z przeciętną, z maksimum lub z minimum.

*

Jeżeli chodzi o wagi, to najczęściej żąda się spełnienia przez system wag dwóch warunków:

Inaczej mówiąc: wagi powinny być nieujemne oraz sumować się do 1. Ten drugi warunek po prostu ułatwia obliczenia.

Czasami wagi przyjmuje się arbitralnie, na wyczucie. Można np. rozważać cztery wskaźniki (rentowność netto, płynność bieżąca, zwrot z kapitału i rentowność brutto na sprzedaży) i wymyślić sobie, że zwrot z kapitału jest tak ważny, iż dostaje wagę 3/4, a pozostałe trzy cechy dzielą między siebie 1/4, więc każda dostaje 1/16. Naturalnie za taką decyzją powinno stać jakieś uzasadnienie. Nie zawsze jednak mamy pomysł, co zrobić, więc możemy przyjąć wagi jednakowe:

To jednak wnosi niewiele: wszystkie cechy ważą tyle samo. Można zatem wykorzystać narzędzie statystyczne:

V_z(x_j) to współczynnik zmienności j-tej zmiennej. Jest to iloraz odchylenia standardowego i średniej arytmetycznej. Współczynnik ten przyjmuje wartości od 0 do 1 - i jeśli jest wysoki, to uznajemy, że cecha jest mocno zróżnicowana. Często się uznaje, że dzieje się tak powyżej 0,6 pkt. (powyżej 60 proc.). Jakkolwiek by nie było, idea wag określonych w ten sposób jest taka: dzielimy współczynnik zmienności j-tej zmiennej (cechy) przez sumę tych współczynników dla wszystkich cech. W efekcie najważniejsze staną się te cechy, które są najbardziej zróżnicowane. Stoi za tym pewna logika: jeżeli np. wszystkie badane firmy mają bardzo podobną płynność, to trudno traktować ją jako miarę charakterystyczną i dużo mówiącą. Ale jeżeli np. rentowność netto jest bardzo zróżnicowana (co niekoniecznie oznacza bardzo duży rozstęp...), to pozwala ona odróżniać od siebie firmy.

*

Normalizacja zmiennych, jak powiedzieliśmy na początku, to bardzo złożone zagadnienie. Kilka innych wariantów normalizacji opisaliśmy w artykule nt. metody MOORA. Ogólnie rzecz biorąc, w naszych tekstach nt. MCDM (oraz w artykułach analitycznych, w których praktycznie te metody wykorzystujemy) czytelnik znajdzie liczne przykłady standaryzacji, unitaryzacji i ważenia danych.

Adam Witczak


BIBLIOGRAFIA:

M. Balcerowicz-Szkutnik, E. Sojka, "Metody ilościowe w finansach i rachunkowości", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2011.

S. Bartosiewicz, M. Otorowski, Budowa i analiza TMAI dla spółek notowanych na Giełdzie Papierów Wartościowych, https://docplayer.pl/586411-Budowa-i-analiza-tmai-dla-spolek-notowanych-na-gieldzie-papierow-wartosciowych.html

J. Michnik, "Wielokryterialne metody wspomagania decyzji", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013

M. Nowak, "Metody ELECTRE w deterministycznych i stochastycznych problemach decyzyjnych", Decyzje nr 2, grudzień 2004

A. Pieloch-Babiarz, Ocena atrakcyjności inwestycyjnej spółek giełdowych odpowiedzialnych społecznie, Zarządzanie i Finanse - Journal of Management and Finance, vol. 13, no. 1/2015

E. Roszkowska, T. Wachowicz, "Metoda TOPSIS i jej rozszerzenia - studium metodologiczne", w: "Analiza wielokryterialna. Wybrane zagadnienia", seria "Informatyka w badaniach operacyjnych", Wydawnictwo Uniwersytetu Ekonomicznego w Katowicach 2013.

W. Tarczyński, Rynki kapitałowe - metody ilościowe, Agencja Wydawnicza "Placet" 1997