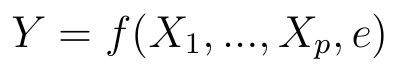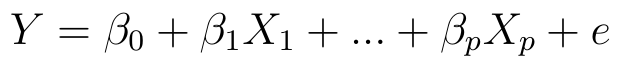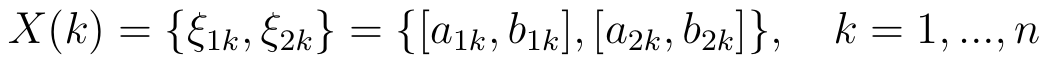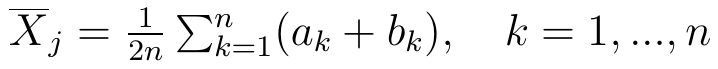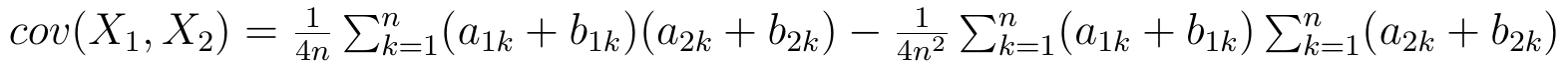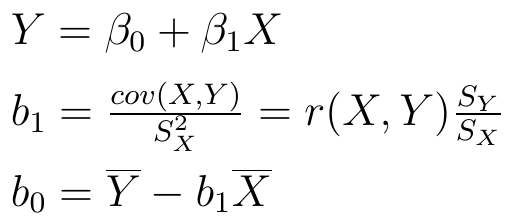Regresja przedziałowa

Regresja liniowa to jedna z najprostszych i najbardziej popularnych metod sprawdzania czy też przybliżania zależności między zjawiskami, w tym np. trendu w czasie. Idea jest prosta - i już ją omawialiśmy na naszych łamach, np. w artykule o kanałach i wstęgach w analizie technicznej. Okazuje się bowiem, że niektóre narzędzia analizy wykresów (np. kanały Raffa) są powiązane z linią regresji, budowaną przy pomocy metody najmniejszych kwadratów.

W największej ogólności idea jest taka: mamy pewną liczbę zjawisk, dla uproszczenia przyjmijmy na razie, że dwa: np. upływ czasu (zmienna X) i przychody przedsiębiorstwa (zmienna Y). Albo: wzrost człowieka z pewnej grupy (X) i jego wagę (Y). Chcemy - na podstawie cząstkowych danych, np. dotyczących tylko niektórych osób, albo niektórych chwil - znaleźć wzór, który będzie w miarę dobrze przybliżał zachowanie zmiennej Y w oparciu o zmienną X. Przyjmujemy przy tym, że ma to być wzór prostej, a więc obrazujący zależność liniową. Tak naprawdę ta zależność jest zwykle inna, ale jeśli dane - gdyby przedstawić rzecz na wykresie - są w miarę blisko tej prostej, to możemy szukać wartości Y dla nieznanych X-ów, zakładając, że z grubsza trafimy prawidłowo.

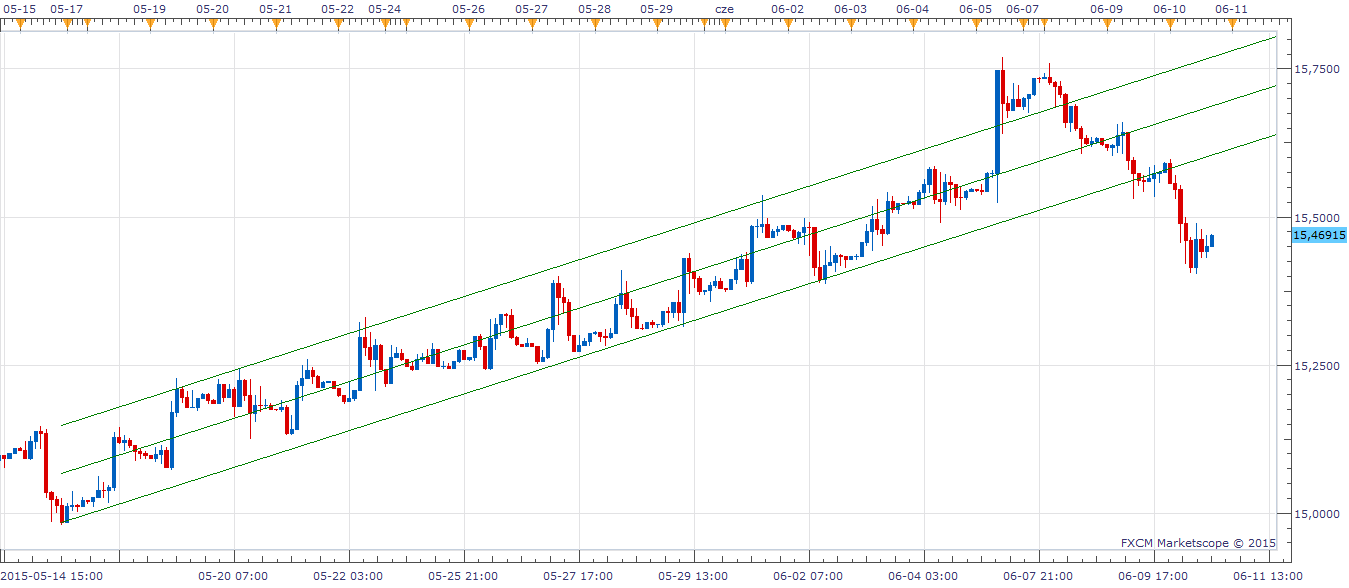
Zresztą, dobrze widać to na rysunku, przedstawiającym wykres z rynku forex - i naniesiony nań kanał Raffa.

Otóż środkowa prosta (czy też półprosta) to właśnie prosta regresji, wyznaczona w oparciu o dane (kursy) z pewnego okresu. Jak widać, faktyczne kursy przez długi czas odbiegały od niej tylko nieznacznie. Prosta ta przez wiele dni dobrze przybliżała trend. Jest ona wyznaczona w taki sposób (przy pomocy odpowiednich metod matematycznych), że zminimalizowana jest suma kwadratów odległości euklidesowych punktów od niej (od tejże prostej). Innymi słowy, inna prosta będzie "średnio" trochę dalej, trochę gorsza: suma kwadratów odległości będzie większa. Sumuje się kwadraty, żeby każda odległość była dodatnia (bez tego mielibyśmy odległości dodatnie - dla punktów "powyżej" prostej; i ujemne - dla tych "poniżej").

Więcej o prostej regresji, metodzie najmniejszych kwadratów oraz o kanałach Raffa - we wspomnianym już tekście z analizy technicznej. W dalszej części artykułu zakładać będziemy, że czytelnik rozumie przynajmniej podstawową koncepcję.

*

Wyobraźmy sobie, że nie dysponujemy dokładnymi, pojedynczymi liczbami (jako wartościami zmiennych X i Y), ale jedynie ich przybliżeniami w postaci przedziałów (zakresów). Na przykład wiemy, że w okresie od 1 marca do 15 maja 2017 liczebność kolonii pingwinów wahała się od 1050 par do 1200 par, zaś od 25 kwietnia do 7 czerwca - od 970 do 1250 par (dane są zmyślone na poczekaniu, nie ręczymy za ich sensowność z biologicznego punktu widzenia). I tak dalej dla kilkunastu czy kilkudziesięciu innych okresów. Zauważmy przy tym, że okresy te mogą się na siebie nakładać, nie muszą następować po sobie, mogą też być między nimi przerwy, nie jest też powiedziane, że populacja w danym czasie stale rosła lub stale malała. Po prostu: mamy obserwacje zmiennych X i Y, a każda taka obserwacja to para przedziałów.

Czy na podstawie takich nietypowych danych można zbudować prostą regresji i coś sensownego przybliżyć? Okazuje się, że tak. W każdym razie paru autorów takie rozwiązania przedstawiło. My bazować będziemy głównie na pracy M. Gliwy "Analiza regresji dla zmiennych symbolicznych", a w szczególności na wzorach opracowanych przez L. Billarda i E. Didaya.

Formuły te są mniej lub bardziej arbitralne. To znaczy: nie jest do końca jasne, co w przypadku danych przedziałowych powinniśmy uznać za średnią arytmetyczną, wariancję czy kowariancję. Zresztą, tak samo jest w przypadku zwykłych danych liczbowych: tyle że od wielu dekad przyjmujemy pewne ugruntowane definicje tych pojęć. Dla danych przedziałowych takiego standardu nie ma, są raczej pewne propozycje. Jedną z nich przedstawimy.

*

Na początku powiedzieliśmy, że zmiennych może być więcej niż dwie. Istotnie, w ogólności interesuje nas taki model:

Mamy p zmiennych objaśniających (X_p) i jedną zmienną zależną (mianowicie Y). Pewna zależność funkcyjna f wiąże je ze sobą. W zależności tej określoną rolę gra też czynnik losowy e.

Interesują nas funkcje liniowe, a zatem de facto rozważamy następujący schemat:

Przyjmijmy teraz, że nasze X₁, ..., X_p to zmienne przedziałowe. Przez ξ_jk = X_jk rozumiemy k-tą obserwację j-tej zmiennej (taka obserwacja to przedział). Ograniczmy się znów do dwóch zmiennych. Niech będzie n obserwacji tych dwóch zmiennych, czyli n par. Możemy k-tą parę zapisać tak:

A zatem jest to np. owa liczebność kolonii pingwinów (od a_1k do b_1k) w przedziale czasowym od a_2k do b_2k.

Billard i Diday uważają, że średnią arytmetyczną j-tej zmiennej (z n obserwacji) należy obliczać tak:

Jest to definicja tejże średniej. Możemy przyjąć, że X₁ = Y oraz X₂ = X. Idea jest prosta: sumujemy sumy początkowych i końcowych punktów każdego przedziału, a potem uzyskany wynik dzielimy przez 2n. W naszym przykładzie z pingwinami wynik dla X₁ = Y, tj. dla populacji, byłby taki: [1050 + 1200 + 970 + 1250]/2*2 = 1117.5.

Teraz zdefiniujemy kowariancję zmiennych X₁ i X₂. O kowariancji dla zwykłych danych liczbowych pisaliśmy przy okazji omawiania metody wielokryterialnej TMAI oraz w tekstach o procesach stochastycznych i miarach efektywności portfela.

Dla danych przedziałowych przyjmujemy taki wzór (w istocie jest on wyprowadzony, przy pewnych założeniach, z dużo bardziej ogólnej formuły, opartej o zdefiniowaną w pewien sposób funkcję gęstości oraz całki podwójne):

Formuła jest na pozór skomplikowana, ale nie wykraczamy poza dodawanie, mnożenie i dzielenie.

Następny wzór to odchylenie standardowe. Dotyczy ono jednej zmiennej (tzn. każdej z osobna), dlatego indeksy przy a i b to jedynie k, a nie indeksy podwójne.

Tu mała uwaga: w pracy M. Gliwy pierwszy ułamek we wzorze to 1/4n, co na pozór wygląda rozsądnie, jako symetryczne z drugim ułamkiem, ale odbiega od wszystkich pozostałych źródeł, do których dotarliśmy. W szczególności wzór w takiej formie jak powyżej, jest pokazany (i wyprowadzony) w oryginalnej pracy Billarda i Didaya (str. 22, wzór nr 29).

Mamy już zatem średnią, kowariancję i wariancję (czy też pierwiastek z niej, tj. odchylenie standardowe). Po co to wszystko? Otóż przy użyciu tych formuł oblicza się współczynniki b₀ i b₁, które są estymatorami współczynników β₀ i β₁ z ogólnego wzoru na zależność Y od X.

Widzimy to poniżej:

Wzory te są takie same jak dla zwykłych danych liczbowych, tyle że "w środku" mamy średnią, odchylenie i kowariancję dla przedziałów.

Spróbujmy zastosować te formuły dla pewnych danych. Nie będzie to jakieś szczególnie głębokie badanie statystyczne: w szczególności nie przetestujemy żadnej hipotezy. Chodzi jedynie o podstawienie wartości do wzorów.

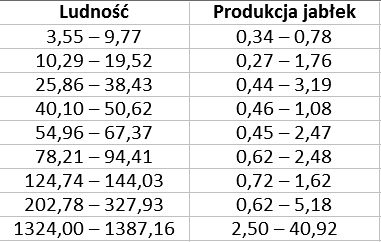
Skorzystamy z prawdziwych danych: o produkcji jabłek przez różne kraje oraz o ludności tych krajów. Materiał obejmuje 40 krajów, a nie wszystkie istniejące. Informacje dotyczą zasadniczo roku 2015, choć ludność w niektórych przypadkach to jedynie teoretyczna estymacja lub wynik z lat późniejszych. Dla naszych celów nie jest to istotne: i tak nie sądzimy, by wolumen rocznej produkcji jabłek dało się realnie uzależnić tylko od liczby mieszkańców kraju.

Oto i zebrane informacje po nadaniu im charakteru przedziałowego. To ułożenie w klasy przeprowadziliśmy dość arbitralnie i na oko, ale - jak sądzimy - w zgodzie ze zdrowym rozsądkiem. Zresztą, to nie problem: gdyby przyjąć, że mamy pełne, pojedyncze odczyty, to moglibyśmy skorzystać ze zwykłej regresji. Tu zachowujemy się tak, jakby cały nasz zasób wiadomości ograniczał się do liczb przedziałowych. Takie dostaliśmy (z jakichś powodów) - i z takimi pracujemy. Dodajmy jeszcze, że dane zaprezentowaliśmy w mln, tak więc np. 40,92 jako produkcja jabłek to 40,92 mln ton (to roczny wynik Chin), a 3,55 jako ludność to 3,55 mln - i to akurat liczba mieszkańców Mołdawii. Zauważmy jeszcze, że przedziały produkcji nakładają się na siebie, a pomiędzy przedziałami ludności są luki. To również nie stanowi problemu.

Po dość prostej, ale pracochłonnej obróbce danych w języku R uzyskaliśmy następujące wyniki (przybliżone):

cov = 2595.84
varX = 238024.1
b1 = 0.0109
sredniaY = 3.66
b0 = 1.235

To oznacza, że wyznaczona prosta ma wzór Y = 1.235 + 0.0109X. Niestety, dane z Chin i Indii dość mocno zaburzają resztę informacji (zwłaszcza chińskie, z gigantyczną produkcją jabłek, nawet po uwzględnieniu przewagi ludnościowej). Problem nie wynika jednak z przedziałowości: podobny pojawiłby się przy zwykłej regresji dla wyjściowych danych. M. Gliwa przedstawia w swoim tekście inne przykłady, w tym również dotyczące kilku zmiennych (np. Y zależy od X₁, X₂, X₃ i X₄), wykazując również (przy pomocy testu statystycznego Studenta) przewagę zaprezentowanego modelu przedziałowego nad innymi, które uwzględniają np. tylko górne lub dolne granice tychże przedziałów.


Adam Witczak

BIBLIOGRAFIA:

L. Billard, E. Diday, "Symbolic Data Analysis: Definitions and Examples", http://www.stat.uga.edu/sites/default/files/images/Symbolic%20Data%20Analysis.pdf

A. Irpino, Basic univariate and bivariate statistics for symbolic data: a critical review, https://arxiv.org/pdf/1312.2248.pdf

M. Gliwa, "Analiza regresji dla zmiennych symbolicznych", w: "Warsztaty doktoranckie '08. Zarządzanie - Finanse - Ekonomia", Wydawnictwo Akademii Ekonomicznej w Katowicach 2009.

W. Xu, "Symbolic Data Analysis: Interval-Valued Data Regression", https://getd.libs.uga.edu/pdfs/xu_wei_201008_phd.pdf